
Cada 15 días, ofrecemos un nuevo acertijo para poner a prueba tu razonamiento lógico-matemática. Las soluciones son publicadas en la misma nota una semana después.
Acertijo 1
Carlos vive solo y llega a la noche apurado a su casa, después de su trabajo, con un apetito aterrador. En ese momento recuerda que a la mañana puso la nueva llave de su casa, sin discriminar, en el llavero de su cintura, que contiene muchas llaves más, todas iguales, tipo Yale.
Como la promesa de un bife con huevos fritos y papas lo tortura, Carlos quiere entrar a su casa lo más rápidamente que pueda.
Se desea saber cuál estrategia de selección de llaves será más eficiente:
- Probar “a lo loco”, desesperadamente, una llave de su llavero en la cerradura.
- Probar cada llave de a una y descartar la que no sirve.
Acertijo 2
Sea p un número primo mayor que 3.
Probar que 24 divide a p2 – 1.
Acertijo 3
La teselación y sus muchas propuestas.
“Teselar” es un verbo que significa cubrir y viene del latín tessela. Por ejemplo: cubrir un piso con mosaicos es teselar el piso. Decorar un friso cubriéndolo con celdas de formas diversas, también es teselar.
Naturalmente, hay otras superficies no planas que interesa teselar.
Por muchos y diversos motivos, el problema de la teselación ha despertado gran interés en el mundo contemporáneo de las matemáticas.
Al respecto, el cubrimiento decorativo con mosaicos de todo tipo se puede admirar en muchas obras de la cultura mora, como este teselado en mayólicas que existe hoy en los interiores de muchas casas de familia de Europa o de nuestra América del Sur, o en edificios que tienen esa inspiración:

Por supuesto, los ejemplos de teselados de otras culturas son muchos. Como los teselados romanos:

O los siguientes teselados andaluces:

Y no se puede dejar de mencionar el teselado en obras más recientes, como las que encaró el artista neerlandés Maurits Cornelis Escher (1898-1972).


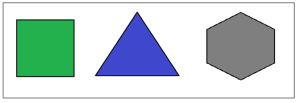
Las teselaciones del plano son, quizás, las más sencillas: las que se generan a partir de algunos polígonos regulares. Por ejemplo, inmeditamente abajo se presentan tres teselaciones del plano, de izquierda a derecha, usando triángulos equiláteros, cuadrados o hexágonos regulares.
Todos hemos visto embaldosados con losetas triangulares, o bien, los más comunes, formados con baldosas cuadradas o hexagonales.
Entre estos tres teselados elementales, la trama del teselado con hexágonos regulares aparece en algunas situaciones especiales que en principio parecen algo desconectadas entre sí, por ejemplo:
En la manufactura textil, a escala industrial o casera, gracias al llamado punto jersey, constituido por una abigarrada red de pequeños hexágonos regulares entrelazados. Estos minihexágonos se pueden ver con el auxilio de una lupa, tomando el tejido y observando sus celdas de cerca.
En la construcción y diseño de enormes espejos para telescopios espaciales como el Telescopio Espacial James Webb, donde sus celdas hexagonales se apoyan en una superficie levemente combada, como es la cúspide de un paraboloide de revolución:

Y por último, en la arquitectura natural usada por las abejas en la construcción de sus panales, que será destinada luego para la custodia de su miel.

Acertijo:
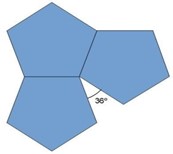
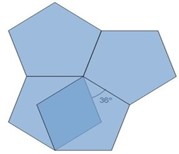
Demostrar que, de todos los polígonos regulares, solamente hay tres que teselan con sus celdas el plano. Ellos son: el triángulo equilátero, el cuadrado y el hexágono regular.
La demostración del problema 3 es más sencilla de lo que alguien podría pensar. Se sugiere concentrarse en los vértices de los polígonos candidatos. No hay que tener miedo de dibujar polígonos regulares sobre un papel y cortarlos con una tijera, para ver qué es lo que sucede.
Acertijo 4
Sean dados un triángulo equilátero, un cuadrado y un hexágono regular, los tres de área 1. Probar que el perímetro del hexágono regular es menor que el perímetro del cuadrado y el perímetro del triángulo equilátero.
Acertijo 5
Es posible que algunos lectores de esta columna se sorprendan por la falta de fórmulas matemáticas que presenta hoy la misma. De hecho, solo se exhibirá —sin demostración— una sola y sencilla fórmula de tres sumandos, tal como se verá tras lo que sigue.
Supongamos que estamos probando un dron terrestre o rover en una zona desértica muy poco habitada con una fauna única que se quiere proteger, tal como la sabana de Kenia o como algún helado sector de la Antártida.

El objetivo es seguir la trayectoria de la huella que deja el dron terrestre sobre el terreno, tarea que se hace con un satélite o con un dron helicóptero, cuya misión preasignada consiste en ejecutar el correspondiente video de la trayectoria del vehículo sobre tierra.
El dron de la foto tiene cuatro ruedas, pero para simplificar supondremos que el vehículo deja un solo trazo continuo sobre la superficie del movimiento.
Por razones de control logístico, el rover dejará una señal circular roja en las siguientes situaciones:
- al comienzo y al final del recorrido,
- en los momentos de detención (destinados a recargar sus baterías solares,
- y en los puntos donde cruce su propia huella.
Como ejemplo, las trayectorias dejadas por el rover podrán parecerse a las dos siguientes, y a muchas variantes más:
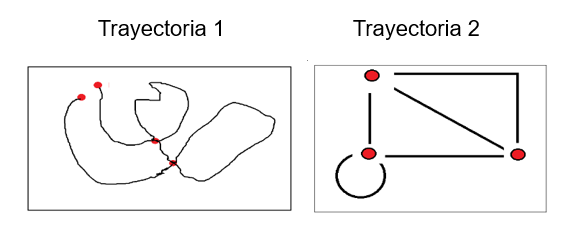
La idea entonces será marcar con un circulito el comienzo y fin de la trayectoria, como así también los cruces de la trayectoria consigo misma.
Tales puntos se llamarán vértices, y al conjunto de vértices lo notamos con V.
Obsérvese, además, que en el grafo de la trayectoria 2 (T2) el vértice de inicio coincide con el vértice de terminación, y no interesará averiguar cuál es cuál. No hay ningún impedimento para que esto suceda.
En la trayectoria 1 (T1) se observa que hay 4 vértices, mientras que en la T2 hay 3 vértices.
Los contornos cerrados, más el espacio plano que contiene a la trayectoria (encerrado por el recuadro rectangular negro), se llaman caras. Al conjunto de caras las notamos con C. Observamos que en el grafo de la T1 hay 3 caras, y observamos que en T2 hay 4 caras.
Los segmentos de arcos entre vértices se llaman aristas, y al conjunto de aristas lo notaremos con A. En T1 hay 5 aristas y en T2 hay 6 aristas.
Una trayectoria como la aquí considerada se llama grafo de Euler, en honor al distinguido matemático Suizo Leonhard Euler, que lo estudió exhaustivamente.
Quiero observar aquí que la definición de “grafo de Euler” dada arriba es meramente operativa, y está simplemente orientada para facilitar el acceso a las ideas interesantes de la teoría.
Es común que el símbolo de numeral # se use para expresar la cantidad de elementos en un conjunto determinado. Luego, si X es un conjunto cualquiera, #(X) designará la cantidad de elementos del conjunto X.
En un grafo de Euler se cumple el siguiente
Teorema de Euler
(TdE)
#(V) – #(A) + #(C) = 2
que en esta entrega aceptamos sin demostración.
Verifiquemos que la ley de Euler citada se cumple para T1 y T2
Para T1: #(V) = 4; #(A)=5 y #(C) =3.
Luego:
#(V) – #(A) + #(C) = 4 -5 +3 = 2
Para T2: #(V) = 3, #(A) = 5 y #(C) = 4
Luego:
#(V) – #(A) + #(C) = = 3 – 5 + 4 = 2
Las dos cuentas hechas sobre las trayectorias T1 y T2 muestran que los grafos definidos por T1 o T2 son ambos grafos de Euler.
La teoría de grafos es muy extensa, y está notablemente desarrollada. Algunas de sus áreas de aplicación incluyen:
- Ingeniería: La TdG se utiliza para modelar y analizar redes de transporte como carreteras, ferrocarriles y redes eléctricas. También se utiliza para diseñar circuitos electrónicos y redes de comunicaciones, tales como la red submarina internacional de internet.
- Ciencias de la computación: La TdG se usa para analizar y aproximar soluciones al problema del viajante de comercio. En este caso, los vértices son ciudades y las aristas, las rutas que unen esas ciudades. En algún momento hablaremos sobre este tema, que tiene mucho interés para las ciencias de la computación.
- Economía: La TdG se usa para modelar redes económicas y de transporte, utilizándose la teoría, también, para estudiar el fenómeno de la estabilidad económica.
Hay aplicaciones también de la TdG en sociología y biología.

Varios suizos han sido verdaderos maestros en el área de las matemáticas. Algunos son miembros de una sola familia, como es el caso de los Bernoulli. Y otro surge en soledad: Leonhard Paul Euler.
A Euler se lo conoce desde el vamos por el llamado número de Euler “e”, que es la base de los llamados logaritmos naturales.
Este hombre excepcional realizó muchos aportes en las áreas del análisis matemático, el álgebra, la teoría de números, y la teoría de grafos, que hemos apenas mencionado aquí, en esta entrega.
Su obra es extensísima. Tanta, que en los años 1970-1980 se estimaba a priori capaz de generar una colección de 80 volúmenes.
Dada la importancia cultural y científica de ese legado, el Gobierno Federal Suizo, en 2000 decidió oficialmente encarar su publicación.
Se cree hoy que tan magno proyecto, denominado Euler-Edition, finalizará hacia 2040. El objetivo gubernamental es publicar la totalidad de las obras de Euler, tanto en formato electrónico como en papel, a título de contribución del pueblo de la Confederación Helvética a la cultura universal.
Hasta la fecha se han publicado 75 volúmenes de la edición electrónica, que incluyen la totalidad de los escritos científicos de Euler, así como una selección de sus cartas y otros documentos personales. Es interesante señalar que los volúmenes se publican en formato PDF, y están disponibles en línea de forma gratuita.
La publicación de la edición en papel está prevista que abarque 100 tomos. Los primeros de estos se publicaron ya en 2015, y cabe decir que hasta la fecha se han publicado un total de 25 tomos en papel.
El acertijo:
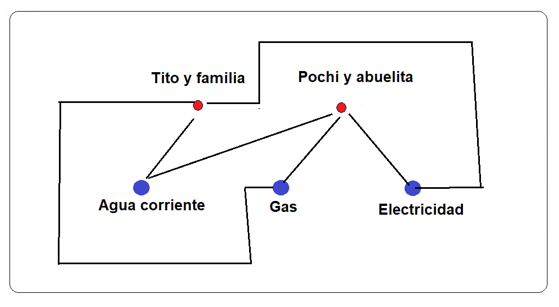
En un remoto e inaccesible caserío llamado Villa Escarpada viven muy pocas personas. Allí, dos grupos de vecinos, constituidos uno por Tito y su familia, y otro por Pochi y su abuelita, han aceptado abonarse a los nuevos servicios de agua corriente, electricidad y gas. Como el suelo es escarpado y posee fallas geológicas, las líneas de suministro no deben superponerse ni cruzarse entre ellas.
Se pide diagramar la conexión de tales tres servicios a los usuarios solicitantes. Una vez realizado, verificar que el diseño satisface las condiciones de seguridad exigidas, que es una manera figurada de pedir que el grafo consecuente cumpla con el Teorema de Euler citado más arriba.
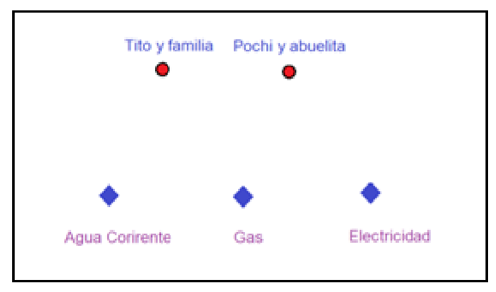
Respuesta
Acertijo 6
Este problema llegó al Río de la Plata más o menos hacia 1964, al mismo tiempo que el inolvidable tema Love Me Do.
Hay un lugar vecino, cercano a Villa Escarpada, igual de difícil por su terreno y por sus montes.
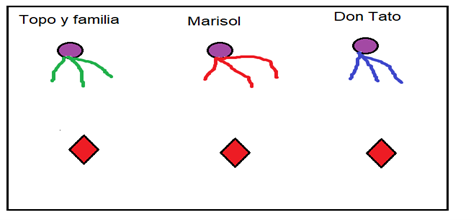
Se trata de Villa Cañadones. Allí han aparecido tres grupos de personas, también interesadas en recibir en sus pequeñas casitas los tres servicios mencionados de electricidad, agua corriente y gas. Se trata de Topo y su familia, de Marisol y de Don Tato.
Se pide a los lectores entusiastas que diseñen una red de suministro de los tres servicios para los tres vecinos de Villa Cañadones.
Respuesta
Acertijo 7
El boceto de Leonardo conocido como El Hombre de Vitruvio ha sido difundido y reproducido en muchos lugares diferentes. Lo he visto reproducido sobre algunas prendas, como remeras o camisolas; también en tapas de discos o calcomanías para la luneta de los autos, o bien para los tanques de nafta en las motos choperas, por citar algunos pocos ejemplos.
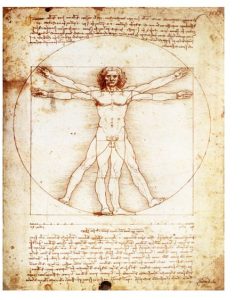
Su completo es Marco Vitruvio Polion y vivió entre los años -80 y -15. Fue un arquitecto romano que trabajó al principio para Julio César. Después se dedicó a la ingeniería civil y también al diseño de diversas construcciones que se llevaron a cabo en su época. Cabe destacar que escribió lo que se considera el tratado de arquitectura más extenso de la antigüedad, desarrollado en 10 tomos, y llamado precisamente De Architectura.
En esta obra, Vitruvio establece la teoría de que el hombre, como criatura, y en muchos sentidos, es la medida de todo lo que lo rodea. Se trata de una idea muy antigua, que tal vez hoy pueda parecer de naturaleza cósmica exagerada. Sin embargo, como principio filosófico, existe desde mucho antes, por ejemplo, desde la época de Pitágoras (-570, -490).
Como sea, la percepción de Vitruvio permaneció en los tiempos sucesivos de manera a veces latente y a veces viva, pero resurgió con fuerza inusitada muchos siglos después, en el Renacimiento con Leonardo, y en el siglo XX con el distinguido arquitecto franco-suizo Le Corbusier, tal como se puede observar en su clásico tratado Le Modulor (1948, 1953), con el cual se piensa hacer en el futuro una entrega especialmente dedicada.

En la presente, vamos a desentrañar algunos de los detalles antropométricos de El Hombre de Vitruvio. Son muchos, alrededor de 20, pero en este caso reflexionaremos solamente sobre dos de ellos, protagonizados por la circunferencia y el cuadrado, que circunscriben y acompañan desde 1490 al Hombre, de acuerdo con los detalles que siguen a continuación.
El Hombre de Vitruvio está concebido en dos posiciones:
Primera posición: Con los pies juntos, en posición de “firmes”, y brazos extendidos, de manera perpendicular a la columna vertebral.
Segunda posición: Con los pies abiertos en un ángulo de 60º y brazos extendidos de manera oblicua hacia arriba, hasta el nivel de la cabeza.
Luego, en primer término, sea el Hombre de Vitruvio en su primera posición.
Obsérvese que, si se considera al Hombre momentáneamente como un ave, la envergadura de sus brazos extendidos es igual al lado del cuadrado en el que está inscripto. Y como el lado superior de tal cuadrado es tangente a la cabeza, y su lado inferior es tangente a sus pies en “firmes”, es inmediato observar que la envergadura de brazos del Hombre de Vitrubio es igual a su altura. El centro de simetría del cuadrado está ubicado en los genitales, cosa que se puede verificar de inmediato con el borde rectilíneo de una hoja de papel.
Sea ahora el Hombre de Vitruvio en su segunda posición.
Se observa que hay una circunferencia que pasa por cada una de las extremidades, cuatro en total: ambos pies en posición oblicua y ambas manos extendidas, ya que los pies en firmes no se consideran. Este hecho tiene ya algo extraordinario, pues se sabe de la geometría euclídea que una circunferencia queda determinada únicamente con tres puntos diferentes, no alineados. En tal sentido, cuatro puntos pueden ser inútiles para dibujar una circunferencia que contenga a los mismos, pero no es este el caso.
Luego, en el Hombre de Vitruvio, la circunferencia está sobredeterminada, como si esa figura estuviese reforzada con un dato adicional, de yapa, que en principio no es necesario para el trazado de la circunferencia circunscripta.
El concepto que sigue es esencial para relacionar al cuadrado con el círculo.
Acerca del Número Áureo
En el boceto de Leonardo, el llamado número áureo aparece en diversos sectores del Hombre, pero como se dijo más arriba, en esta entrega analizaremos tan solo los casos asociados con las dos posiones mencionadas.
Sea entones un segmento cualquiera de longitud finita sobre el plano. Los extremos de tal segmento están señalados con circulitos rojos, pero el punto medio, que nos interesa ubicar, es amarillo:
 Se desea cumplir con la siguiente misión:
Se desea cumplir con la siguiente misión:
Misión Áurea
Lo que se quiere hacer es dividir el segmento (1) en dos partes, de medidas a y b, de tal manera que la medida total (a + b) sea a su parte de medida mayor a, como la parte de medida mayor a sea a su parte de medida menor b. Es decir, la ubicación del punto c deberá cumplir:
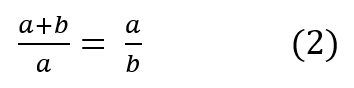 A cualqueira de los cocientes de la igualdad en (2) se lo llama razón o sección áurea.
A cualqueira de los cocientes de la igualdad en (2) se lo llama razón o sección áurea.
La solución a la cuestión planteada en la “misión áurea” brindará la posibilidad de ubicar corectamente al punto señalado con el circulito amarillo c, que cumplirá entonces el objetivo encomendado.
Luego, al interpretar algebraicamenre lo planeado por la misión, vamos a plantear la ecuación que se deriva de la misma.
Desde el inicio en (2) será:
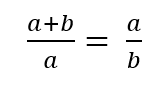
O sea:

Luego, llamaremos x al segundo miembro de (3), para aprovechar que ese cociente expresa adecuadamente a la razón buscada:

Pero todavía no conocemos el valor numérico de x. Entonces con (3) y (4) tenderemos:

Ahora (5) define una ecuacion cuadrática

que posee dos soluciones, de las cuales una es positiva. La misma es generalmente notada con la letra griega “phi” (fi) , cuyo valor es
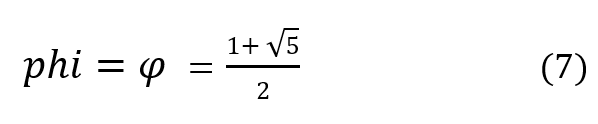
El número “phi” se llama número áureo y también razón o proporción áurea. Tal razón satisface lo planteado en la “misión áurea” de más arriba, es decir
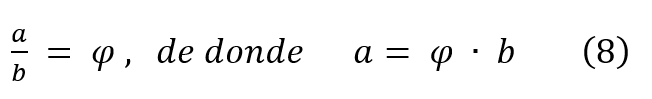
La sección áurea en la primera posición
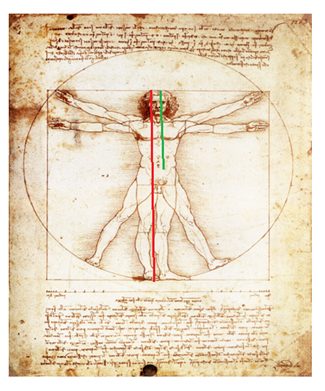
La primera aparción de la sección áurea en el Hombre de Viturvio se observa en el segmento definido por el borde superior de su cabeza y el extremo de sus pies firmes
El segmento en rojo se ha mostrado levemente corrido hacia la izquierda, dejando a la vista el ombligo, para facilitar la percepción de la divisón. Este punto, el ombligo, divide al segmento rojo corespondiente de manera áurea. En tal segmento, la parte inferior entre el piso y el ombligo equivale al segmento de medida a en la figura (1) y el segmento entre el ombligo y el borde superior de la cabeza equivale al segmento de medida b en la misma figura.
La sección áurea en la segunda posición
La segunda posición del Hombre, vincula al cuadrado con la circunferencia de la siguiente manera.
Construyamos un segmento similar al señalado en (1):
 en donde ahora, en la parte de la izquierda, el número a es la medida del lado del cuadrado y en la parte de la derecha, el número b es la medida del radio del círculo.
en donde ahora, en la parte de la izquierda, el número a es la medida del lado del cuadrado y en la parte de la derecha, el número b es la medida del radio del círculo.
En el boceto del Hombre los segmentos aludidos pueden observarse en el esquema siguiente:
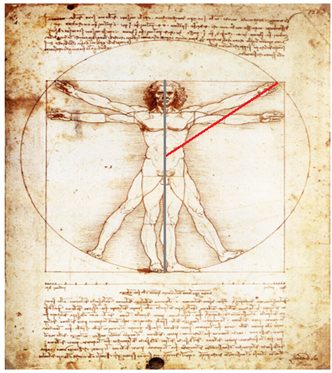
Con el borde de una hoja de papel, para tomar las medidas sobre los segmentos en verde y en rojo, se observará que el cociente entre la medida del lado del cuadrado y la medida del radio del círculo están en proporcion áurea.
Cabe preguntarse, entoces, si las proporciones y secciones acá descriptas existen en la morfología y contextura de un hombre o mujer comunes contemporáneos.
En el siglo XIX y también en el siglo pasado, se han hecho extensos estudios sobre muestras grandes de personas, para confrontar las proporciones del Hombe de Vituruvio con los datos obtenidos de los individuos pertenecientes a un grupo humano homogéneo, en particular. Como respuesta, se ha encontrado que las proporciones del Hombre aquí dadas se cumplen en la realidad solamente en un sentido estadístico aproximado.
Es importante aclarar que el número áureo está íntimamente relacionado con la llamada Sucesión de Fibonacci, que analizaremos y aplicaremos exensamente más adelante. Los valores iniciales de esta sucesión son dos: 0 y 1, mientras que los siguientes, se generan con la suma de los dos anteriores. La sucesión de Fibonacci empieza así:
0, 1, 1, 2, 3, 5, 8, …
Al respecto, es necesario comentar que desde 1960 existe una prestigiosa revista académica trimestral, The Fibonacci Quarterly, que estudia estos temas y otros afines, con el mayor nivel científico.
El acertijo
Dados tres puntos en el plano, no alineados, dibujar la única circunferencia definida por ellos. Explicar cómo es el procedimiento.
En el texto de arriba, en (9) se muestra que el número áureo phi satisface
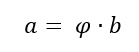
Mostrar también que
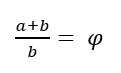
Acertijo 8
Otra vez un círculo y un cuadrado acoplados
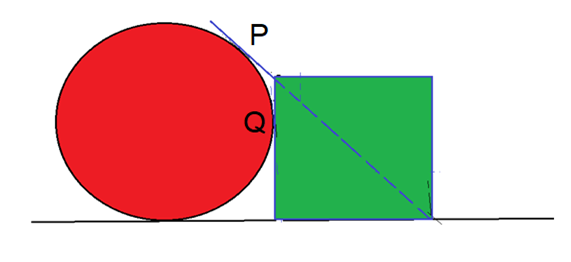
El dibujo muestra un círculo (en colorado) de radio unidad, apoyado sobre una recta horizontal. A su derecha, aparece un cuadrado (en verde), también apoyado sobre la misma recta de base, cuyo lado izquierdo es tangente al círculo colorado en el punto Q, pero de tal manera que la diagonal “noroeste-sudeste” del cuadrado es también tangente al círculo, en el punto P.
Se pide hallar el área del cuadrado.
Acertijo 9

Desde hace ya muchos años, ha aumentado la cantidad de personas que creen que nuestra vieja Madre Tierra es una especie de panqueque que flota a la deriva en el Cosmos, y que vuela en ese entorno exótico, tal vez inescrutable, tal vez hechizado y sumamente rebelde.
Esa gente adhiere a la Teoría de la Tierra Plana. En las crónicas, en los medios, en internet, sus adherentes se llaman terraplanistas. Y son bastantes.
Una consulta al respecto con Bard, la IA de Google, arrojó la siguiente respuesta:
Es difícil estimar con precisión el número de terraplanistas que existen en el mundo, ya que no hay una organización central que los represente. Sin embargo, según algunos estudios, la cifra podría oscilar entre los 10.000 y los 100.000 personas.
La mayoría de los terraplanistas se encuentran en los Estados Unidos, donde la Flat Earth Society (Sociedad de la Tierra Plana), la organización más importante de este movimiento, tiene su sede. Sin embargo, también hay terraplanistas en otros países, como el Reino Unido, Australia, Canadá y Brasil.
El movimiento terraplanista ha ganado popularidad en los últimos años, gracias al auge de las redes sociales y a la difusión de teorías conspirativas en internet. Los terraplanistas suelen argumentar que la Tierra es un disco plano, que está rodeada por un muro de hielo. También creen que el gobierno y las agencias espaciales ocultan la verdad sobre la forma de la Tierra.
Hay varias razones por las que las personas creen que la Tierra es plana. Algunos lo hacen por motivos religiosos, ya que creen que la Biblia describe una Tierra plana. Otros lo hacen por motivos conspirativos, ya que creen que el gobierno oculta la verdad sobre la forma de la Tierra para controlar a la población. También hay personas que simplemente se sienten atraídas por lo exótico y lo desconocido de la idea de que la Tierra es plana. Independientemente de las razones, los terraplanistas constituyen un movimiento de personas que se niega a aceptar la evidencia científica que demuestra la esfericidad de la Tierra.
Mucha gente honrada, sin embargo, piensa en esta cuestión, y en sintonía con lo que expresa la IA, también ha buscado con calma las características propias de tal creencia, en un momento en donde, al mismo tiempo, hay robots que escarban por cascotes en la Luna, también en la fosa de las Marianas, o equipos de científicos que piensan en cómo desviar un asteroide de su órbita potencialmente peligrosa. Esa gente sabe que existieron antiguos héroes del conocimiento, y de la acción, que fundamentaban sus argumentos con lógica y que eran maestros de la observación de la realidad natural y de la consecuente indagación científica.
Eratóstenes y la Biblioteca
Uno de tales héroes fue Eratóstenes de Cirene, quien nació en el año -276 y murió en Alejandría hacia el año -104. Hay indicios que cuentan que Eratóstenes fue nombrado director de la Biblioteca de Alejandría por el Faraón Ptolomeo II Filadelfo, alrededor del año -236.
Tal biblioteca fue fundada años antes por Alejandro, tras su paso por Egipto, y llegó a ser la institución más notable de su época, no solamente por la cantidad de libros atesorados allí, sino también por las indagaciones científicas que se llevaban a cabo en su seno.

Debido a la incidencia de fuertes intolerancias políticas y también religiosas, de las que lamentablemente somos testigos también en nuestro tiempo, la biblioteca fue incendiada en algunas oportunidades, hasta que con el correr de los años decayó y desapareció para siempre, alrededor del año 390 de nuestra Era.
En 1995, en un interesante esfuerzo conjunto internacional dirigido por la UNESCO, pudo inaugurarse en Alejandría —con gran pompa— una Biblioteca muy bien diseñada, con la intención de recordar u homenajear la pasada gloria de la antigua cultura helenística que brilló en ese lugar.
La proeza de Eratóstenes
En algún momento, Eratóstenes oyó decir que al comienzo del verano, en la ciudad de Asuán, al mediodía, los obeliscos del lugar no generaban sombra, como que los rayos de la luz solar incidían de manera perpendicular sobre el terreno.
Sin embargo, a la misma hora, en Alejandría sus obeliscos sí generaban sombra, pues los rayos solares no incidían verticalmente sobre los mismos, sino que lo hacían con una inclinación de 7,2º, hecho que se puede apreciar esencialmente en la figura 1 de abajo.
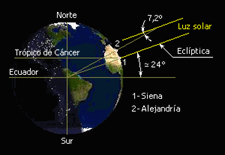
Eratóstenes supuso acertadamente que la superficie terrestre estaba curvada entre las dos ciudades.
La curvatura sospechada por Eratóstenes podría deberse, por ejemplo, a un fenómeno de deformación geológica local en el continente africano, o tal vez, tal efecto angular podría haber sido causado por la curvatura propia local de nuestro cuerpo planetario, dotado de una forma arbitraria y desconocida, como por ejemplo la que tiene una alfombra arrugada.
Sin embargo, debido a la incidencia de principios filosóficos básicos relacionados con el pensamiento platónico, Eratóstenes supuso que nuestro planeta podría ser esférico.
Y si fuera así, entonces se propuso calcular su radio.
Esto requirió un esfuerzo logístico de considerable magnitud, pero la tarea se llevó a cabo con éxito total.
Eratóstenes diseñó y construyó un odómetro, es decir, un instrumento mecánico concebido para medir distancias sobre el terreno. Y munido de tal herramienta, realizó efectivamente el viaje entre las dos ciudades midiendo la distancia entre las mismas.

No he podido ubicar ninguna ilustración acerca del instrumento utilizado por Eratóstenes, pero sí conseguí detectar un odómetro romano del s. II. Y para dar una idea de la evolución tecnológica acaecida en este tema, también incluyo a su lado, abajo, un odómetro contemporáneo con visor digital, apto para tareas profesionales muy precisas de agrimensura.
Ahora bien, una vez efectuado su viaje, la lectura de su instrumento le permitió conocer a Eratóstenes que el valor de la distancia entre Alejandría y Asuán era aproximadamente de 843 kilómetros. Como se comprenderá, este valor se ha expresado en unidades contemporáneas, dado que en Egipto era usual la antigua unidad llamada “estadio”, equivalente a 157,5 metros, en el actual sistema métrico decimal.

Es debido a esta tarea que a Eratóstenes se lo considera por lo general como el padre de la Geodesia.
Esta disciplina se dedica a describir la forma y medidas de la Tierra, así como otros aspectos complementarios que tienen que ver con la Cartografía y la Geofísica planetaria.
Muchos brillantes matemáticos y físicos se han dedicado a la Geodesia, como Carl F. Gauss (1777-1855), Friedrich W. Bessel (1784-1885), Pierre Simón de Laplace (1749-1827), Adrien Marie Legendre (1752-1833), Giovanni Cassini (1625 -1712), Isaac Newton (1642 -1727), George Gabriel Stokes (1819 -1903), Veiko Alexander Heiskanen (1895-1971), y varios otros más.
Cabe observar que el razonamiento de Eratóstenes es correcto porque el Sol se encuentra muy lejos de la Tierra, alrededor de unos 150 millones de km. Esta distancia hace que los rayos que inciden sobre la superficie de nuestro planeta lo hagan de manera paralela.
Si el Sol estuviese cerca de la Tierra, la hipótesis de los rayos paralelos no sería válida y entonces los cálculos de Eratóstenes arrojarían un valor erróneo. Se sugiere pensar en esta observación.
Acertijo
Sobre la base de los datos obtenidos por Eratóstenes, según el relato de esta entrega, en conjunto con la información que figura más arriba en la Figura 1, se pide obtener el valor aproximado del radio de la esfera terrestre. Y ya que estamos, hallar también el valor, en kilómetros, de la circunferencia de nuestro planeta.
Acertijo 10
El matemático estadounidense Richard Courant (1888–1972) cita en su famosa obra Qué es la matemática una anécdota de Eratóstenes.
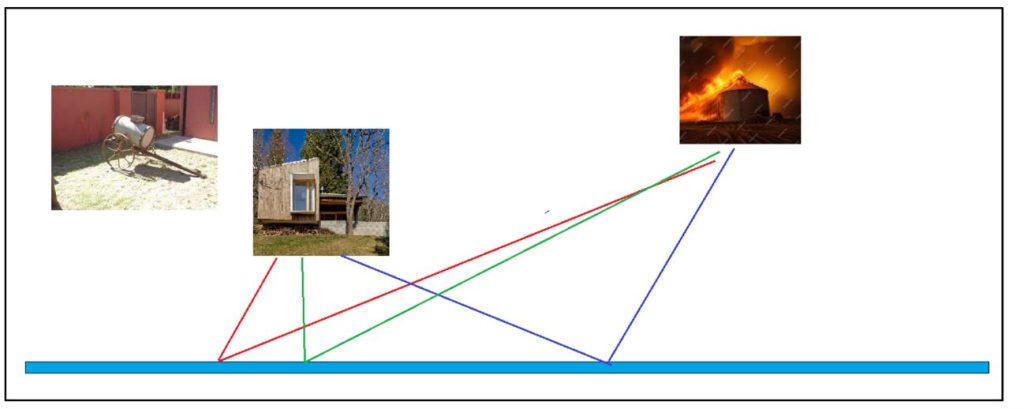
Eratóstenes tiene una casita de descanso, cerca de un pequeño arroyo, representado por la franja azul en el dibujo de arriba. También tiene un silo. De repente, ese silo comienza a incendiarse. Por suerte, al lado de su casita, Eratóstenes tiene un carrito aguatero.
Lo que tiene que hacer Eratóstenes es tomar el carro, ir al arroyo, cargarlo de agua, y salir para el silo con el objeto de rociarlo del preciado líquido. Esta tarea se puede hacer a través de varias trayectorias, como lo señala el dibujo. ¿Cuál es la trayectoria más conveniente de todas?
Acertijo 11
La bella Guillermina está tendida de manera muy cómoda sobre un amplio sofá y mira muy interesada, en su tele gigante frontal, un partido amistoso de fútbol entre la selección paraguaya y la selección argentina.
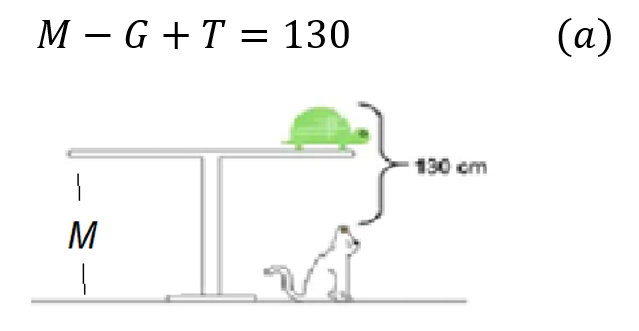
En ese momento, su gato Titán está sentado al lado del sofá, abajo de una mesa semiratona, y mira el partido con el mismo entusiasmo que su ama. Sin embargo, la otra mascota, la tortuga Wanda, duerme plácidamente arriba de la mesa, ajena a todo el barullo ambiental.
La distancia entre la caparazón de la tortuga Wanda y las puntas de las orejas de Titán es de 130 cm., tal como lo indica la figura de abajo:
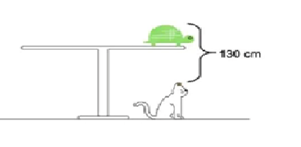 Una señal musical de la jarra térmica en la kitchenette avisa a Guillermina que ya está lista el agua para el mate, con lo que la niña se ausenta por algunos segundos.
Una señal musical de la jarra térmica en la kitchenette avisa a Guillermina que ya está lista el agua para el mate, con lo que la niña se ausenta por algunos segundos.
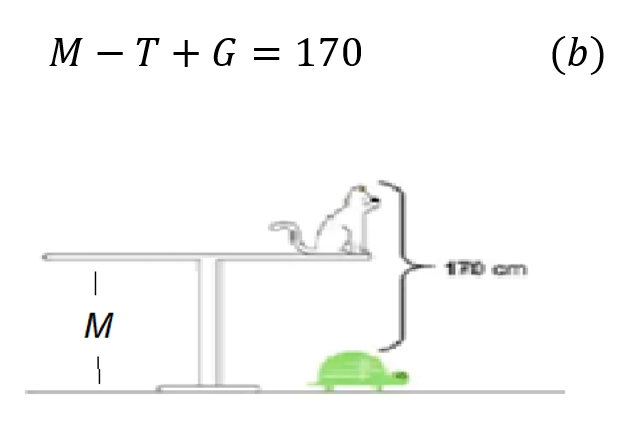
Y con mucha premura, ya a con todo el equipo de mate renovado, vuelve Guillermina para sumergirse de nuevo en la acción. En el acto, observa que su gato Titán está algo incómodo con su ángulo de visión y decide cambiar a sus bichitos de lugar. Además, Wanda, sin afectarse para nada, sigue durmiendo con igual placidez.
Debido al cambio impuesto por Guillermina, la métrica en los elementos del conjunto de mascotas ha cambiado. Ahora, la distancia entre la punta de las orejas de Titán y la caparazón de la tortuga Wanda es de 170 cm., tal como lo muestra la figura inmediatamente más abajo.
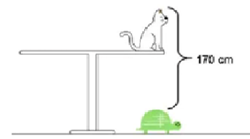
Pero entonces, a dos minutos de finalizar el partido, en el área chica albiceleste, una tremenda chilena del delantero albirrojo Antonio Sanabria clava la pelota en el ángulo superior derecho del arco albiceleste y vence al Dibu Martínez, arquero argentino.
¡¡La selección de fútbol de Paraguay ha ganado por 1 a 0!!
Entonces, en medio de la algarabía dominante, esta columna de acertijos pregunta a sus lectores cuál es la altura de la mesa de Guillermina.
Acertijo 12
En la primera aparición de esta columna vimos un problema de aritmética.
Acá va otro parecido:
Demostrar que si n ≥ 1, entonces 6 divide a
![]()
Acertijo 13
Pensado para los lectores más jóvenes de CdS.
Un señor viudo es profesor de matemáticas en la secundaria de la pequeña ciudad de Itanará. Cabe observar también, que tal vez sin quererlo, dicho señor es muy denso con sus dos hijos adolescentes mellizos, Juani y Tobi, porque los satura a cada rato con interrogantes de carácter matemático.
Los dos chicos ya no saben qué hacer, pues entienden que su padre es un gran tipo aunque sumamente pesado con su manía didáctica para con ellos.
Pero el profesor, a pesar de ciertamente ser lo señalado con sus chicos, no es tonto ni malo. Sabe desde hace bastante tiempo que Tobi se ha entusiasmado totalmente con una bellísima guitarra Fender Stratocaster, en acabado “sunburst” (“ráfaga de Sol”) combinada con un potente equipo Marshall, ambos de EE. UU., inabordables para su economía. 
Similarmente, Juani, desde hace varios años, anda como loco por poseer una pistola de aire precomprimido Steyr, austríaca, en calibre 4.5mm, apta para competencias de tiro olímpico como las que se organizan en el Polígono de Asunción, igualmente inabordable para sus finanzas a priori.
En cierta oportunidad, después del cole, el señor los llama para conferenciar y les dice:
-Chicos, los llamo para informarles que la tía Carlota Eusebia, sí, la de Barcelona, de quien tanto les hablé en otras oportunidades, falleció hace unos meses y me ha declarado su heredero universal. Luego, les comunico que estoy capacitado financieramente para concretar esos bellos deseos que cada uno de ustedes guarda en lo más profundo de sus tiernos corazoncitos. Me refiero a la Stratocaster con su equipo Marshall y a la Steyr de competición olímpica.
 Los chicos coincidieron en un estrepitoso alarido:
Los chicos coincidieron en un estrepitoso alarido:
-¿¿¿¿¿En serio papi?????
-No tan rápido, gurises. Previamente, me tienen que resolver este problemita.
De su attaché, el señor extrajo una caja metálica llena de bellas bolitas cristalinas multicolores. Dijo a continuación:
-Miren esta caja de bolitas y cuéntenlas, por favor.
Y en un santiamén los chicos las contaron. Gritaron al unísono:
-¡¡Son 130 bolitas!!
Y el papá siguió explicando:
-Lo que les pido es esto: ustedes tienen que formar dos subconjuntos de bolitas, uno chico, de cardinal p, y otro grande de cardinal g. Y todo esto, no así a la bartola, de tal manera que 4 veces el cardinal del subconjunto más chico sea igual a la tercera parte del cardinal del subconjunto más grande. Me tienen que decir cuáles son esos dos cardinales.
Y los chicos preguntaron, casi al unísono:
–¿Y qué más, papi?
-Nada más, chicos. Está todo dicho. Yo ya cumplí con mi parte. Ahora les toca a ustedes. Y como es muy tarde, me mandaré a la cucha, a dormir. Cuidadito con ustedes si me llegan a llamar por el celu a esa compañerita que tienen, la Yésica. Lo sé perfectamente, esa alumnita que tiene siempre 10 en mate. Voy a estar atento. ¡Buenas noches!
Los chicos aceptaron el desafío, y se quedaron trabajando en el problema durante la noche, en completa soledad, y gastando largas horas de análisis. Pero, entusiasmados, cumplieron dignamente la tarea antes del amanecer.
¿A qué correcta conclusión llegaron los hermanitos?
Acertijo 14
Especulación acerca de un cilindro cerrado
Sea el cilindro cerrado siguiente de altura h y volumen V, es decir, tanto h ha como V se consideran datos previos:
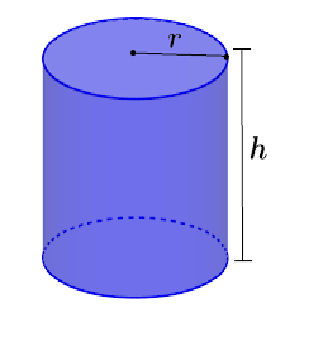
El diámetro de la base d = 2r satisface
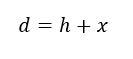
para un cierto valor x que a priori es desconocido.
Se pide hallar una expresión para la superficie total del cilindro en función de h y V.
Acertijo 15
El tema aquí tratado sugiere ser interesante porque muestra cierta interacción —hoy no parece muy frecuente—, entre algunos filósofos y algunos matemáticos.
De manera breve, una supertarea (supertask) consiste en la ejecución, en tiempo finito, de infinitos procesos bien definidos, siempre basados en el sustrato operativo de la lógica proposicional bivalente clásica.
Sí, es cierto: lo que aparece en bastardilla es algo denso. Al respecto, aclaro que lo dicho arriba sobre tal asunto fue tan solo para abrir el fuego sobre esa cuestión.
Sin embargo, estoy seguro de que la inteligibilidad será plena cuando los acertijos especialmente preparados en esta entrega se analicen y se intenten atacar con cuidado.
Pintando los puntos interiores de un recinto 3D
Tombo es filósofo, y además es íntimo amigo de Demi, un matemático algo torpe y distraído.
Son innumerables las pullas y diatribas que se gastan entre ellos, en especial cuando se juntan para jugar al ajedrez o a disfrutar por la tele de un partido de fútbol.
Demi, en este instante, saborea un excelente café en pocillo, preparado por Tere, la mujer de Tombo.
Al mismo tiempo, observa sobre el tablero la posición de su caballo en terreno adversario amenazado por una torre de Tombo.
Dice Demi:
—Tombo, ustedes los filósofos constituyen una banda de chantas absolutos e insoportables. Viven aferrados a Hegel, y como él se pasan la vida diciendo pavadas sin sentido. ¡¡Y les va bárbaro!! Tienen los mejores cursos a cargo, saturados siempre de chicas bellísimas, con unas minis brutales, y ganan guita a rolete… ¡¡¡Y las editoriales de moda, sin objetar, les sacan de las manos esos panfletos espantosos que ustedes escriben y que llaman libros!!! ¡¡Cómo los envidio!!!
Pero Tombo contesta firmemente, ya curtido en este tipo de gastadas por parte de su amigo:
—¿Te parece, Demi? ¡Por decir esas cosas tan inteligentes he aprovechado tu brillo mental para morfarte el caballo! ¡Andá a pedirle al doctor Salamone que te lo clone!
A pesar de la pérdida de su caballo, con bastante esfuerzo, Demi logra que la partida termine en tablas.
Sin embargo, Tombo ha quedado algo alterado por la crítica de su amigo matemático.
Le habla antes que se vuelva para su casa y le dice:
—Demi, quiero que me ayudes en un problema que saqué de la web, y del cual no tengo la menor idea acerca de cómo encararlo. Se trata de una supertarea. Estamos en una sala como esta, pero totalmente vacía de muebles:
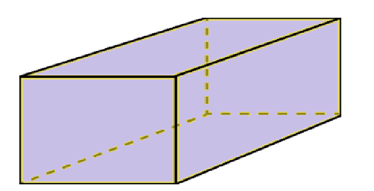
Supongamos que cada punto de esta sala tenga una entidad concreta, real. Me piden pintar cada punto de esta sala de color rojo o bien de color azul, sin ningún patrón y sin ninguna regla. Además, tengo que completar el pedido en cuatro horas. Claramente, eso define una supertarea: un laburo con infinitos procesos (pintar todos los infinitos puntos de la sala) en el tiempo finito de cuatro horas.
Al terminar la supertarea, un punto cualquiera de esta sala vacía será rojo o bien será azul.
Demi interrumpe:
—Dale, sí, ¿y entonces?
—Me tenés que demostrar que en esa sala siempre podés encontrar un triángulo equilátero con los tres vértices del mismo color.
Luego, sin decir nada, pero con una expresión de cierta zozobra, Demi se fue a su casa y pensó.
A la mañana siguiente, ¡¡¡¡llamó a su amigo Tombo con la solución al acertijo!!!!
¿Cuál fue el argumento de Demi?
Acertijo:
Una sala como la del dibujo de más arriba tiene sus puntos interiores pintados de rojo o bien de azul. Demostrar que siempre es posible encontrar en ese recinto un triángulo equilátero con sus tres vértices del mismo color.
Obsérvese que nada se dice acerca de pintar cada punto de la sala con color rojo o azul. Lo dice el problema para generar inquietud, pero la idea es suponer a priori que los puntos de la sala ya han sido pintados de dos maneras, como lo recalca el texto.
Acertijo 16
Algo sobre la Lámpara de Thompson
Este problema fue planteado por el filósofo británico James Thompson, quien lo analizó en 1954. Luego, a partir de ese momento, la literatura específica consecuente lo ha citado como “el problema de la lámpara de Thompson”.

Se lo puede describir como sigue.
Se tienen exactamente 2 horas para realizar este experimento:
Una lámpara se enciende en el instante t = 0 y se la deja así durante 1 hora. (1)
Luego se la apaga durante la mitad del tiempo restante.
Luego se la enciende durante la mitad del tiempo restante.
Luego se la apaga durante la mitad del tiempo restante,
y así sucesivamente hasta que se cumpla la segunda hora de tiempo. (2)
Entonces Mr. Thompson pregunta cuál es el estado de la lámpara, al cabo de haber transcurrido exactamente 2 horas, a partir del instante de haberse iniciado el experimento.
Es decir, Mr. Thompson quiere saber si su lámpara, al cabo de 2 horas, está prendida o apagada.
Vamos a tratar de responderle a Mr. Thompson con rigor absoluto.
En primer lugar, analizaremos la estructura métrica de los intervalos de tiempo en donde se desarrolla el experimento, tal como se lo describe más arriba, entre las llamadas (1) y (2).
Tal proceso, exige realizar una partición del intervalo cerrado de tiempo [1,2] en donde los extremos de los intervalos que establecen dicha partición, están dados por los puntos he dicho Sn definidos como sigue:
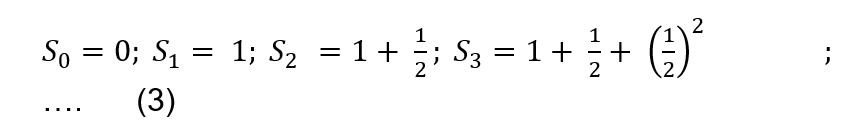
y en general,
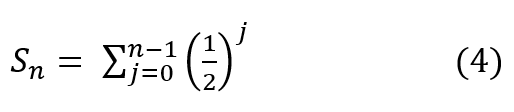 Luego, los intervalos
Luego, los intervalos
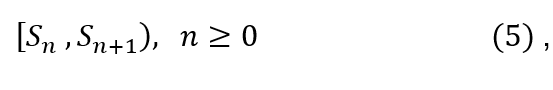
con el agregado del conjunto unitario {2}, son los que definirán la partición del intervalo [0, 2]:
Si en un intervalo como en (5), se verifica que el subíndice n del extremo inferior es par, la lámpara estará prendida. Ese será el caso para los intervalos
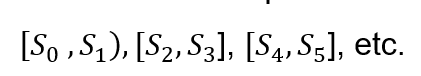
Si, por el contrario, el subíndice n del extremo inferior del intervalo de partición es impar, la lámpara estará apagada. Y ese será el caso para los intervalos
![]()
Los elementos Sn de la sucesión especificada en (3) o (4) constituyen progresiones geométricas de razón ½. Es importante observar que se trata de sumas finitas.
Luego, se puede decir que:

Y así sucesivamente.
El correlato gráfico aproximado para el tiempo del experimento será:

Luego, la partición del intervalo temporal [0, 2] queda realizada como una unión infinita de intervalos cerrados a izquierda, de extremo Sj y abiertos derecha, de extremos Sj+1, con el agregado del singulete [2]. Todo esto permite representar al intervalo [0, 2] como:
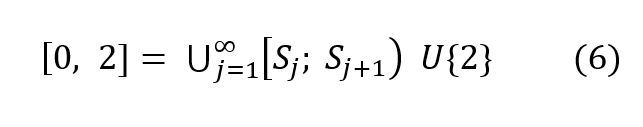
Desde luego, la igualdad conjuntista (3) debe ser probada, cosa que se deja para los lectores interesados, ya que es algo sencillo. El detalle queda “boyando” para no alejarnos del meollo de la cuestión aquí analizada.
La suma (finita) Sn de n primeros términos de la sucesión dada por los extremos de los intervalos de la lámpara de Thompson, tiene una forma cerrada muy conocida, que es la progresión o suma geométrica finita. Puede expresarse así:
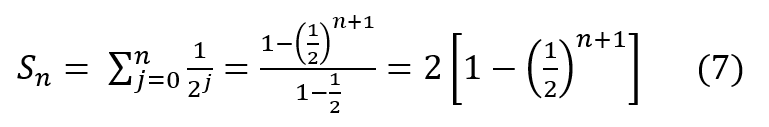
La expresión (7) es la suma de n sumandos una progresión geométrica de razón (1/2). Esto nos permitirá hacer algunas consideraciones finales.
Tal vez la principal es esta:
Para cualquier instante t < 2 se puede saber si la lámpara está prendida o apagada. (8)
La conclusión (8) es cierta pues la expresión (6) permite inferir que para el instante t elegido, existe un intervalito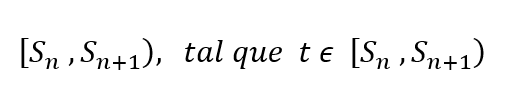
Ahora bien ¿Cuál será el estado de la lámpara en t=2?
Acá debe observarse con énfasis:
El instante t = 2 no es alcanzable de manera finita por la expresión (4), cosa de la que ya se puede sospechar en la igualdad conjuntista (6), donde queda plasmado el intervalo [0, 2].
La expresión “de manera finita” quiere decir que las sumas Sn no alcanzarán jamás el instante 2, en todo el tiempo que le quede de vida al Universo. ¿Pero y si el Universo tiene vida infinita? Tampoco lo alcanzarán.
Aunque atención: fuera del Álgebra, aparece el concepto de punto de acumulación, que es un concepto trans algebraico o sea topológico. Tal realidad permite escribir:
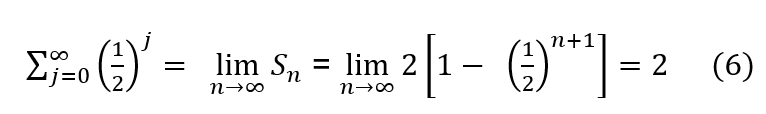
Es decir, el instante 2 es inalcanzable de manera finita por las sumas parciales Sn, pero al mismo tiempo, (6) permite observar que 2 es punto de acumulación de las sumas parciales Sn.
Para reforzar lo dicho, recordemos que
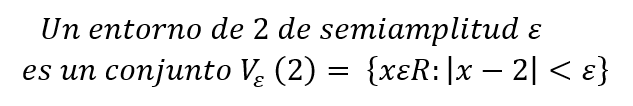
Luego (6) dice que cualquier entorno de semiamplitud épsilon de 2, tiene elementos Sn que son distintos de 2, cualquiera sea la pequeñez de ese tal . Este fenómeno dice, precisamente, que 2 es punto de acumulación de las sumas parciales Sn .
La expresión (6) implica una suma de infinitos términos, y como ya se dijo, su sentido escapa al álgebra, y se define topológicamente de la manera allí dada.
Se recalca que ese fenómeno de aproximación permanente que poseen las sumas parciales Sn al número 2, es inexpresable en términos algebraicos o finitos.
Entonces nuestra respuesta al problema planeado por Mr. Thompson es esta:
Toda la información producida por el sistema de apagado y prendido de la lámpara – antes del instante 2 -, es insuficiente para inferir o deducir, a partir de ella, el estado de la lámpara de Mr. Thompson en el instante 2.
Por supuesto, dicha lámpara puede estar prendida, puede estar apagada, o puede explotar y haber dejado de existir a partir del instante 2. El estado de la lámpara en t=2 es independiente causalmente de lo sucedido con la lámpara antes de ese instante.
NO hay contradicción ni paradoja de ninguna naturaleza en todo lo aquí expuesto.
Y eso es todo.
Al cabo del experimento de la lámpara de Thompson, ¿Cuánto tiempo neto permaneció la lámpara prendida? ¿Cuánto tiempo neto permaneció apagada?
¿Qué te pareció este artículo?

Ricardo Miró
Licenciado en Ciencias Matemática por la Facultad de Ciencias Exactas, Físicas y Naturales de la Universidad de Buenos Aires. Intervino como tal en el área de Estudios Especiales de la petrolera argentina YPF, SE. Luego se desempeñó en el Área Estadística de la Corte Suprema de Justicia de Argentina. Posee varios trabajos publicados centrados en las aplicaciones de las ciencias matemáticas.






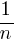 . Si no se toma ninguna medida y se prueba con las llaves del llavero sin ton ni son, resultará que en cada prueba la probabilidad de acertar será invariablemente igual a
. Si no se toma ninguna medida y se prueba con las llaves del llavero sin ton ni son, resultará que en cada prueba la probabilidad de acertar será invariablemente igual a 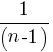 .
.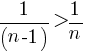
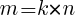
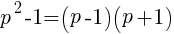 (1)
(1)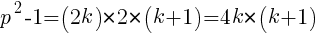 (2)
(2)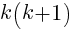 denota el producto de dos números naturales consecutivos, que será fatalmente divisible por 2. Luego
denota el producto de dos números naturales consecutivos, que será fatalmente divisible por 2. Luego 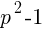 será divisible por 8.
será divisible por 8.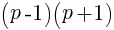 , se puede decir legítimamente lo siguiente:
, se puede decir legítimamente lo siguiente: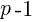 puede ser divisible por 3 o no. Si lo es, nada habrá que demostrar. Pero si no lo es, los restos de la división de
puede ser divisible por 3 o no. Si lo es, nada habrá que demostrar. Pero si no lo es, los restos de la división de 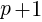 será divisible por 3.
será divisible por 3.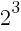 y 3 dividen a
y 3 dividen a 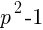 .
.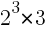 , divide también a
, divide también a 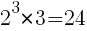 , divide a
, divide a 


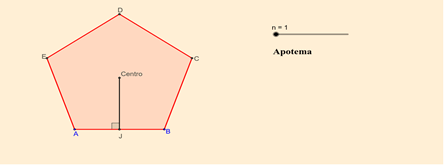
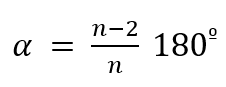
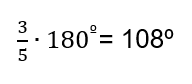
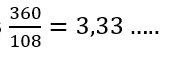
 Usando el teorema de Pitágoras para h, podemos deducir fácilmente que la altura h verifica
Usando el teorema de Pitágoras para h, podemos deducir fácilmente que la altura h verifica
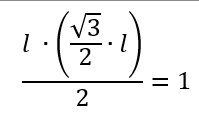
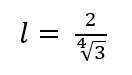

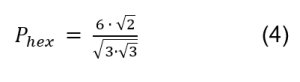
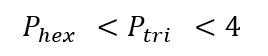
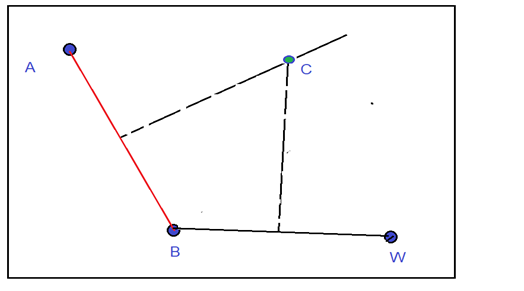 Por tales puntos medios se trazan dos perpendiculares. Cada punto de la perpendicular sobre AB determina un triángulo isósceles que posee dos lados iguales. De la misma manera, cada punto de la perpendicular a BW en su punto medio, determinará otro triángulo isósceles con dos lados iguales. Por lo tanto, cuando esas dos perpediculares se cortan —explicar por qué se cortan—, aparecerá el centro C de la circunferencia buscada.
Por tales puntos medios se trazan dos perpendiculares. Cada punto de la perpendicular sobre AB determina un triángulo isósceles que posee dos lados iguales. De la misma manera, cada punto de la perpendicular a BW en su punto medio, determinará otro triángulo isósceles con dos lados iguales. Por lo tanto, cuando esas dos perpediculares se cortan —explicar por qué se cortan—, aparecerá el centro C de la circunferencia buscada.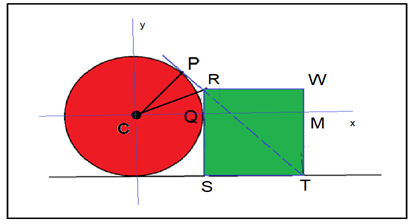
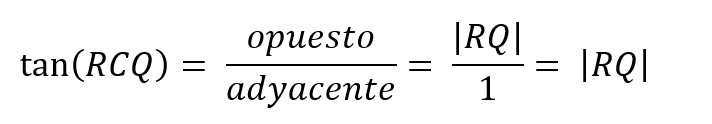

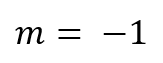
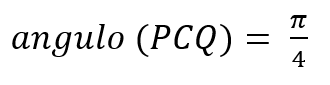
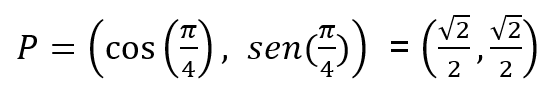
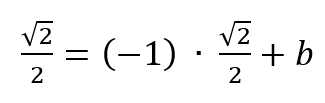
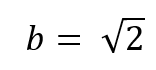
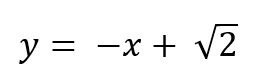
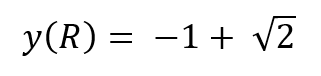
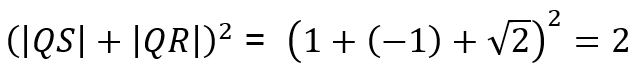 y listo.
y listo.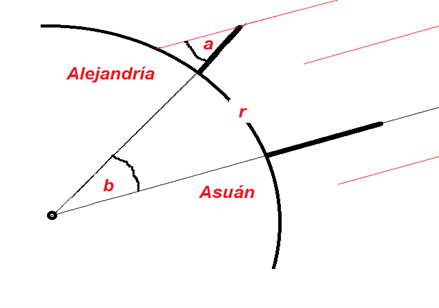
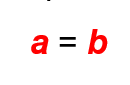 Pero el ángulo b, aunque no pueda determinarese con un transportador, puede calcularse según el llamado sistema radial. En este sistema, un ángulo como el b se mide mediante el cociente entre la medida del arco que subtiende dicho ángulo y la longitud del radio vector. Es decir,
Pero el ángulo b, aunque no pueda determinarese con un transportador, puede calcularse según el llamado sistema radial. En este sistema, un ángulo como el b se mide mediante el cociente entre la medida del arco que subtiende dicho ángulo y la longitud del radio vector. Es decir,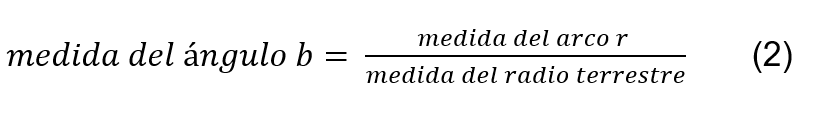
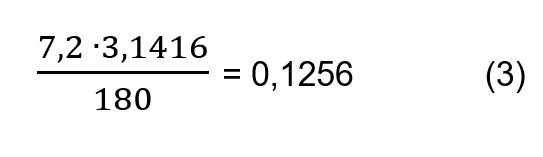
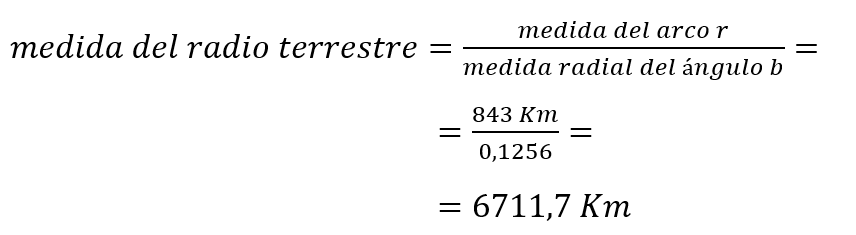 Y a partir de este último valor, podemos calcular de inmediato el valor del diámetro de la esfera terresre y el valor de su circunferencia.
Y a partir de este último valor, podemos calcular de inmediato el valor del diámetro de la esfera terresre y el valor de su circunferencia.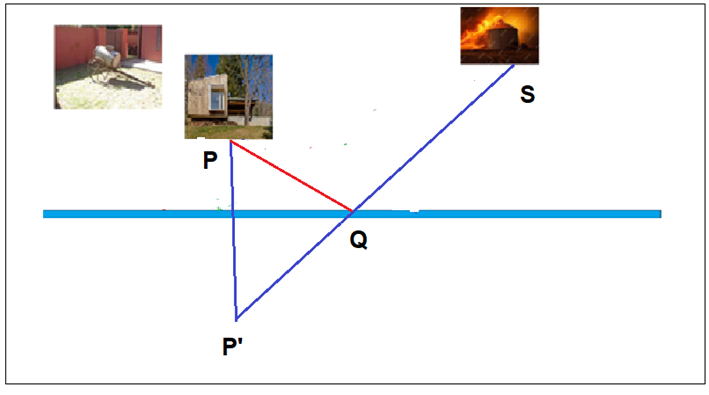
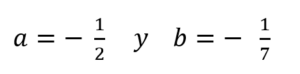
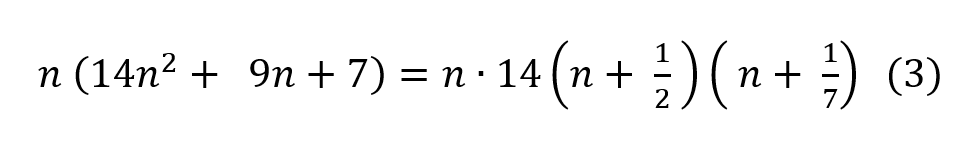
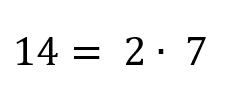
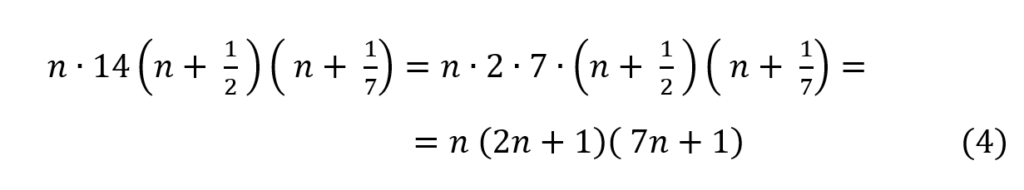
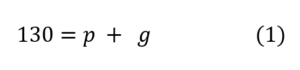


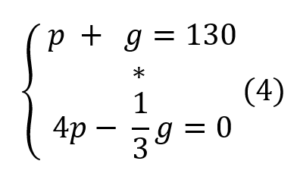 El par de ecuaciones citados al unísono en (4) es un sistema de ecuaciones lineales no homogéneo y caracteriza completamente el problema resuelto por los chicos. Se llama sistema lineal porque todas las incógnitas de dicho problema, p y g, figuran elevadas a la potencia 1, y no homogéneo, pues los segundos miembros de par de ecuaciones (4) no son todos iguales a 0, dado que en la primera ecuación del par se observa el número 130.
El par de ecuaciones citados al unísono en (4) es un sistema de ecuaciones lineales no homogéneo y caracteriza completamente el problema resuelto por los chicos. Se llama sistema lineal porque todas las incógnitas de dicho problema, p y g, figuran elevadas a la potencia 1, y no homogéneo, pues los segundos miembros de par de ecuaciones (4) no son todos iguales a 0, dado que en la primera ecuación del par se observa el número 130.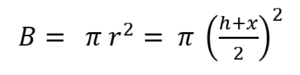
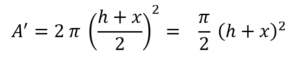
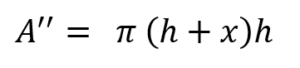
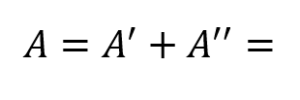
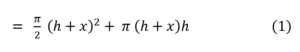
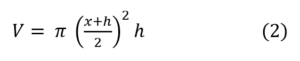
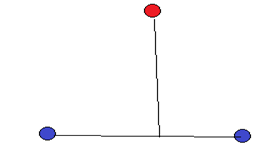 Pero en este caso, empiezo a desarrollar una búsqueda girando en círculo alrededdor del eje de extremos iniciales azules.
Pero en este caso, empiezo a desarrollar una búsqueda girando en círculo alrededdor del eje de extremos iniciales azules.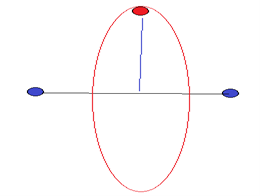 Entonces, en tal caso, inscribo en esa circunferencia un triángulo equilátero cuyos tres vértices tienen el mismo color rojo.
Entonces, en tal caso, inscribo en esa circunferencia un triángulo equilátero cuyos tres vértices tienen el mismo color rojo.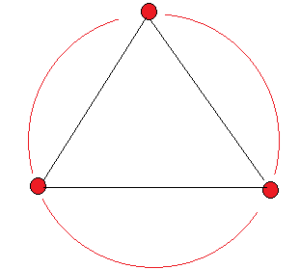
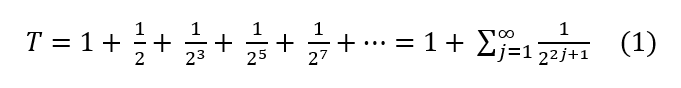
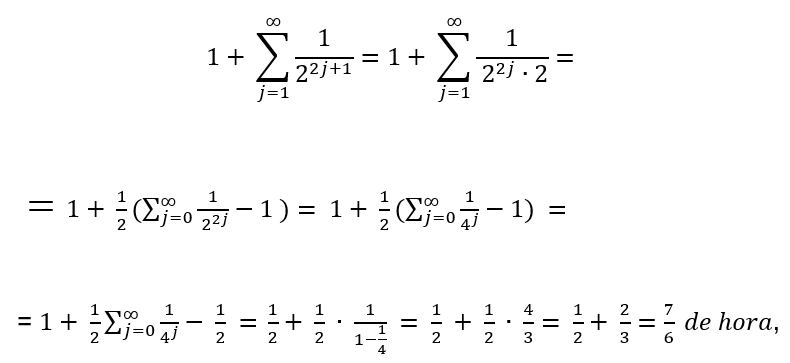

 (12 votos, promedio: 4,92 de 5)
(12 votos, promedio: 4,92 de 5)







Ricardo, amigo, siempre fui una bestia peluda en matemática, pero creo que saqué ambos acertijos bastante rápido. El de las llaves tipo Yale, si Carlos añadió la llave nueva a su llavero a la mañana, ésta solo puede estar en alguno de los dos extremos del conjunto de llaves. De modo que la búsqueda de la llave correcta no es muy a lo loco, sólo hay que comprobar dos. Bife con huevos garantizado. En cuanto al valor de p para satisfacer la ecuación, supongo que es 7, porque su cuadrado da 49 y restando 1 se llega a 48. Si lo saqué yo, lo saca casi cualquiera que esté promediando la escuela secundaria. En cuanto al newsletter, me parece bueno de contenidos y de buen diseño. Te vas a divertir, creo, y contribuir a la cultura científica de la región. Yo también trabajo ad-honorem en AgendAR, así que te entiendo.
Hola, Daniel!!!! Muchas gracias por haber interervenido en el análisis y la lectura de esta columna!!!! Después discutimos, si querés lo que pusiste acerca de los acertijos… Te mandé el link de CdS para que lo vieras, y observes la polenta que tiene esta gente!!! No entiendo cómo Agendar no considera tu larga trayectoria. Muhcas gacias por haberte metido en CdS.!!!!! RM
Acertijo 1: Probar con la última llave que está más cerca del punto donde se insertan las llaves (ej. puntas de la cuerda o el llavero), esa tendría que ser la última llave si no quitó ninguna otra antes.
Acertijo 2: p=5
p2 – 1 = 5^2 – 1 = 24/24 = 1
Estimada Gianina: muchas gracias por participar en esta columna. Sos la primera en hacerlo, y el hecho me descoloca un poco, en el sentido operativo de tal verbo. Necesito explicarte por qué.
Resulta que recién empiezo a colaborar con CdS , y estoy muy poco canchero con su modus operandi interno. He hablado bastante con Daniel, quien me ha explicado como piensa organizar las respuestas a los acertijos de una manera orgánica y sistemática. Por eso, si te contestaea por este medio ahora, es posible que destruya los planes editoriales con respecto a la implementacion especificas de las respuestas.
Te ruego entonces que tengas un poquito de paciencia y esperes unos pocos dias más, a lo sumo cuatro o cinco dias más.
Sería bárbaro que no te borres de esta columna. Como sugerencia primaria me animaría a decirte que pienses otra vez el acertijo 2. Y te repito. Muchas gracias por participar. Quedate cerca porque entre todos vamos a emprender un viaje muy interesante.
Acertijo 2
https://imgur.com/ZlaKYnc
Hola John!!
Muchas gracias por participar en la columna.
En tu respuesta, aprece un link que muestra un ejercicio solamente parecido al aquí tratado. Y es parecido (en realidad es distinto) pues tu ejercicio agrega hipótesis adicionales a la única que ofece el ejercicio 2 de esta columna, que consiste únicametne en considerar a p como primo mayor que 3.
De todas maneras tu aporte es valioso, pues será analizado cuando el Editor largue al aire, dentro de algunos dias, las respuestas a los dos ejercicios. Sería muy piola para todos, muy interesante, que no te borres y que sigas en contacto con esta columna.. De vuelta, muchas gracias por tu envío!!!
.