No solo las obras de arte suelen ser objeto de valoraciones estéticas. Solemos considerar bellos a rostros y cuerpos humanos, animales, paisajes, y edificios. ¿Por qué no también a las teorías científicas?
Cuando decimos que algo es bello, estamos emitiendo un juicio de valor que trata de expresar dos cosas al menos: que el objeto en cuestión ha causado en nosotros un cierto tipo de experiencia, llamada experiencia estética, y que esa experiencia nos resulta placentera.
Existe una gran variedad de experiencias estéticas. Algunas son producidas por sonidos, otras por imágenes, aún otras por meros pensamientos. La caracterización de la experiencia estética desde el punto de vista de la actividad de nuestro cerebro es un área de investigación activa en neurociencias.
Entre otras cosas, las investigaciones muestran que este tipo de experiencias dependen no solo del objeto externo, sino también fuertemente del estado del sujeto, de su educación, de las condiciones ambientales, y mucho más.
Independientemente de las investigaciones teóricas y experimentales sobre el origen del fenómeno estético, el crítico puede identificar un conjunto de propiedades en un objeto de una cierta clase, sea material o conceptual, que parecen correlacionarse muy bien con el desencadenamiento de la experiencia estética. Si el objeto es una obra de arte, probablemente se inscriba en una tradición que ya cuente con ciertas convenciones respecto a las cuales se miden las bondades de la obra.
En el caso de una teoría científica, que es un objeto puramente conceptual no concebido originalmente como una forma de arte, la asignación de belleza puede ser más controversial. Por ejemplo, he conocido personas que consideran la mecánica cuántica como una teoría bella. Otros la sienten insatisfactoria, incómoda y estéticamente abominable (Albert Einstein está entre ellos).

Aún recuerdo la profunda sensación de belleza que sentí cuando por primera vez llegué a comprender la electrodinámica clásica en su formulación covariante, allá por 1986. Siempre he sentido, desde entonces, que la electrodinámica es una de las más bellas teorías de la física. Sin embargo, no todos sienten eso. Por supuesto hablamos de quienes han llegado a entender cabalmente la teoría. Quien no la conoce será indiferente y no le asignará valor estético alguno.
Quien la llegó a vislumbrar, acaso en su forma integral o incluso diferencial pero no covariante, tal vez tenga opiniones estéticas sobre la teoría, pero difícilmente coincidirán con las de quien la conoce en su formulación más completa y elegante.
De todas las teorías de la física, hay una coincidencia prácticamente universal acerca de la belleza de la teoría de la relatividad general, conocida a veces simplemente como Relatividad General (RG).
Por ejemplo, Lev Landáu y Egveny Lifshitz, en su famoso Curso de Física Teórica, afirman sin más que la RG es “la más bella de todas las teorías de la física”.
Lorentz, quien fue uno de los científicos que más influyeron sobre Einstein, manifestó que la teoría tenía el «mayor grado de mérito estético». Rutherford, por su parte, sostuvo que «la teoría de la relatividad de Einstein, aparte de cualquier cuestión sobre su validez, no puede sino ser considerada como una magnífica obra de arte», y Paul Dirac ponderó su “belleza y elegancia”.
El veredicto parece ser unánime: todo aquel que ha estudiado la teoría a fondo coincide con que es una de las más bellas creaciones del ser humano. Confieso coincidir plenamente con semejante fallo. No hay teoría más bella.
Dicho esto, ¿en dónde radica esa belleza? ¿Cuáles son las propiedades de una teoría que hacen que tenga un valor estético además de científico?
Antes de responder, tratemos de esbozar brevemente el contenido de esta obra maestra del pensamiento humano que es la teoría de la relatividad general. Obviamente, una evaluación estética requiere un conocimiento profundo del objeto de apreciación. Lo que sigue son solo unos apuntes breves para dar un contexto al lector.

Una teoría completa y varios años de trabajo
Einstein completó la teoría de la relatividad general el 25 de noviembre de 1915, cuando halló las ecuaciones fundamentales que hoy llevan su nombre. Había estado trabajando más de 7 años, con interrupciones, éxitos parciales y pasos en falso. Partió de un intento de generalizar su teoría de la relatividad especial para que fuese aplicable a cualquier tipo de sistema físico, incluidos aquellos que están sometidos a aceleraciones.
A partir de su formulación del principio de equivalencia, que expresa la identidad de un sistema uniformemente acelerado con un campo gravitacional constante, Einstein comprendió que la nueva teoría sería también una teoría de la gravitación. Durante los años que pasó en Praga como profesor de la Universidad Alemana, Einstein llegó a entender que en la nueva teoría el espacio físico no podría ser descripto por una geometría euclídea, donde la suma de los ángulos interiores de un triángulo es de 180 grados.
A partir de 1913, cuando volvió a la Escuela Politécnica de Zürich como profesor, Einstein trató de formular su teoría por medio de una descripción geométrica en cuatro dimensiones del espacio-tiempo, entidad que había sido introducida en la física en 1908 por Hermann Minkowski.
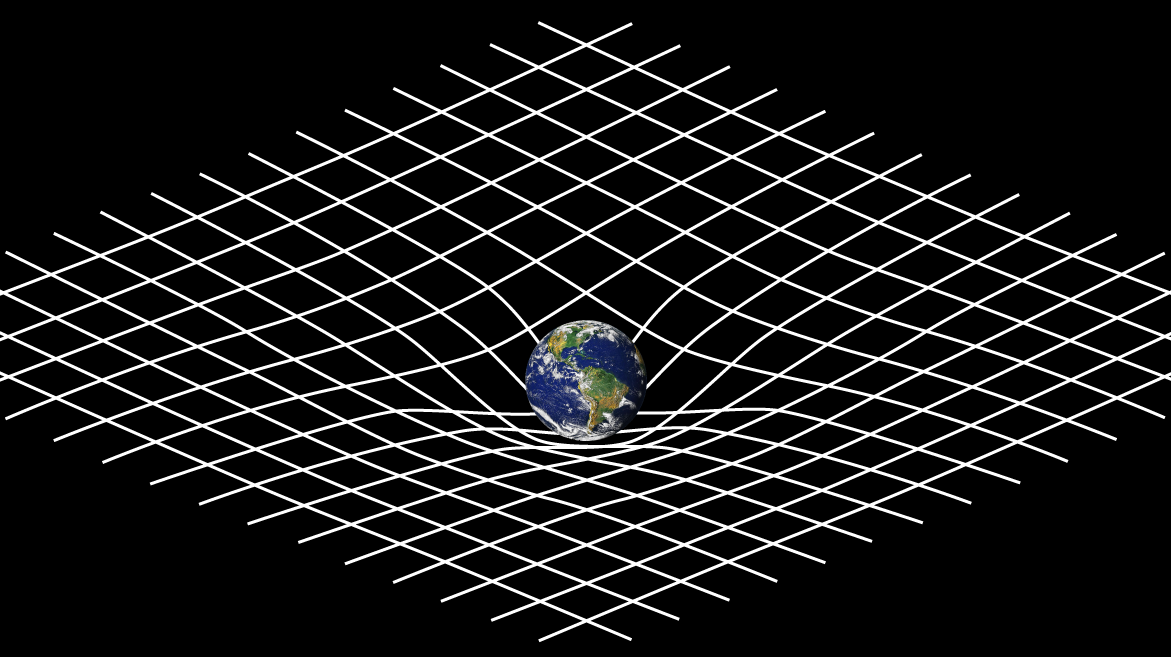
El espacio-tiempo de Minkowski es no euclídeo, pero es el mismo en todos los puntos. El de Einstein interactúa con los objetos que forman el mundo y presenta una estructura geométrica que cambia con la distribución de materia. En otras palabras, la curvatura del espacio-tiempo depende directamente de la distribución de energía y de los movimientos de los sistemas físicos. No es independiente del resto del mundo. A mayor concentración de energía, mayor curvatura.
La curvatura, a su vez, determina el camino más corto entre dos puntos, que en una geometría general (o de Riemann) no tiene necesariamente que ser una recta.
Las ecuaciones que descubrió Einstein en 1915 permiten determinar la curvatura del espacio-tiempo si se conoce la distribución de energía y cantidad de movimiento de los sistemas físicos. Luego, resulta que las trayectorias mínimas en el espacio-tiempo curvo corresponden a las que siguen los cuerpos en presencia de lo que llamamos gravitación.
La nueva teoría es más precisa que la de Newton para describir estos efectos y predecir otros nuevos.
Por ejemplo, si admitimos que el espacio-tiempo es una entidad real, entonces se puede perturbar por el movimiento de objetos muy masivos cuando son acelerados. El resultado es que esas perturbaciones son ondas de curvatura que se propagan a la velocidad de la luz cambiando la forma en que se determinan las distancias localmente.
Se trata de una “onda de gravedad”, descubiertas casi 100 años después de que Einstein predijera su existencia.
La nueva teoría no solo tiene un poder predictivo mucho mayor que la teoría de Newton, sino que elimina la idea de la gravedad como una fuerza de la naturaleza y la reemplaza por un concepto preciso de espacio-tiempo. Espacio, tiempo y gravitación han sido desplazados por un espacio-tiempo de geometría no euclídea.
¿Por qué una teoría como esta causa un profundo sentimiento estético en los que la comprenden? Me atrevo a sugerir que lo que se produce en el cerebro de quienes entienden la teoría es la valorización de las siguientes características:
-
Simplicidad: a partir de un sistema de solo 10 ecuaciones diferenciales de segundo orden no lineales, es posible, en principio, calcular la evolución de cualquier sistema físico cuya energía-momento se especifica. Contrariamente a otras teorías, tanto las ecuaciones de movimiento para la materia como las leyes de conservación pueden obtenerse de las ecuaciones de Einstein. Esto hace que la teoría sea conceptualmente sencilla, pero al mismo tiempo pueda describir procesos en extremo complejos, debido a la no linealidad de las ecuaciones.
-
Simetría: una simetría es una invariancia frente a algún tipo de cambio. La RG tiene el grupo de simetrías más rico de toda la física: sus ecuaciones son invariantes frente a cambios generales de sistemas de referencia. Esto es lo que se expresa al decir que la teoría es “covariante general”.
-
Fuerza de unificación: la teoría elimina la gravitación como campo y la reemplaza por el espacio-tiempo. Tres conceptos que denotan entidades diferentes en la teoría de Newton (espacio, tiempo y campo gravitacional) son reemplazados por el concepto de espacio-tiempo. La gravedad pasa a ser simplemente la manifestación empírica de los cambios de curvatura del espacio-tiempo.
-
Fundamentalidad: dentro de la física clásica, la RG parece ser una teoría absolutamente fundamental. Esto es, no puede obtenerse como caso límite de otra, como sucede con la mecánica de Newton o la termodinámica.
-
Belleza matemática: la teoría aplica una herramienta matemática (la geometría diferencial y el cálculo tensorial) que es notable por su simplicidad y elegancia. Al usar 4 dimensiones en vez de 3, permite tratar en pie de igualdad a todas sus variables (1 temporal y 3 espaciales).
-
Poder explicativo: la teoría permite recuperar los resultados de la teoría de Newton y predecir muchos otros, como ser el corrimiento del perihelio de los planetas, el corrimiento al rojo de la radiación en presencia de objetos masivos, la deflexión de la luz por el Sol y otros astros, la óptica gravitacional, las ondas de gravedad, y mucho más.
-
Fuerza lógica: la teoría puede deducirse de unos pocos postulados y no presenta problemas serios de interpretación, como es el caso, por ejemplo, de la mecánica cuántica.
La presencia de cualquiera de estas características en una teoría científica tiende a producir reacciones estéticas en aquellos que pueden apreciarlas. La conjunción de todas resulta en que la RG sea considerada la más bella de las teorías.
Para terminar, agrego un punto señalado por el propio Einstein, quien escribió: “Una modificación de la misma [la RG] parece imposible sin la destrucción del todo”. Este es el atributo al que los teólogos llaman perfección. Perfecto es aquello que es disminuido por el cambio. Por cualquier cambio.
De allí que para Tomás de Aquino la inmutabilidad es un atributo divino. En los grises días de noviembre de 1915, Albert Einstein parece haber intuido, para ventura nuestra, ese modo de la divinidad.
¿Qué te pareció este artículo?
Columnista y miembro del Consejo Directivo de Ciencia del Sur. Doctor en física por la Universidad Nacional de La Plata (UNLP). Actualmente es Investigador Superior del CONICET, Argentina y director del Instituto Argentino de Radioastronomía (CONICET, CICPBA, UNLP). Además, se desempeña como Profesor Titular de Astrofísica Relativista en la UNLP. A la par de su trabajo como científico, es investigador en filosofía. Entre sus libros se destacan Introduction to Black Hole Astrophysics (con G.S. Vila, Springer 2014) y Scientific Philosophy (Springer, 2018). En 2019 fue nombrado Graduado Ilustre de la UNLP.
Dirige un grupo de investigación de más de 20 personas que trabajan en astrofísica, cosmología y teoría de la gravedad. Es uno de los científicos más influyentes de la Argentina por su productividad académica.








 (60 votos, promedio: 4,73 de 5)
(60 votos, promedio: 4,73 de 5)






Un bellísimo comentario para una teoría elegante
Finalmente pude leer el artículo, y me sorprende el hecho de que he sentido tal fascinación por diversas teorías relacionadas mas con el campo químico (acaso sea por mi especialización en el área); sin embargo la Ley de Gravitación de Newton siempre me había parecido estremecedoramente bella, superada solo por la Relatividad General. Muy preciso el concepto, y de muy amena lectura. Como siempre gracias por enriquecer mi conocimiento general. Saludos!
En la filosofía, la belleza de un filosofar puede tener muchas direcciones; en cuanto a su lenguaje poemático (Nietzsche, Platón) a su claridad explicativa (Aristóteles, San Agustín) o a su oscuridad fascinante (Heráclito, Deleuze)
En la capacidad para sintetizar en sentencias o máximas, verbigracia; «yo soy yo y mis circunstancias» de Ortega y Gasset o «Cogito ergo sum» de Descartes.
Es difícil, establecer parámetros, o por lo menos implica un esfuerzo mayúsculo. Pero, en lo que a mi respecta, una de las bellezas que más me cautiva es la capacidad para visualizar horizontes distintos de los mismos problemas.
Excelente artículo muy motivador y accesible.
No entiendo como un sistema de «solo» 10 ecuaciones diferenciales de segundo orden no lineales pueda ser simple, cuando un sistema de menos ecuaciones de primer orden no lineales ( a veces linealizables), puede dar cabida a sistemas caóticos (sistemas complejos).
De otro lado no me resulta extraño que en un universo (linealizado) aunque solo sea bajo el lenguaje tensorial, la parte creativa la hagan las curvaturas.
¿ de donde tanta alharaca por el hecho simple de que las figuras geométricas
( que se caracterizan por una curvatura) sean independientes del sistema lineal de referencia desde el cual las observamos?