Desde la antigüedad, el movimiento de los astros ha despertado el interés del ser humano y grandes científicos como Copérnico, Galileo, Kepler y Newton dedicaron gran parte de su trabajo a estudiarlos.
El francés Henri Poincaré fue uno de los matemáticos más reconocidos en la historia. En 1890 otro prestigioso matemático, Mittag-Leffler, organizó un concurso desafiando a los científicos de la época a resolver el problema gravitacional de los N-cuerpos.
El problema se puede describir de la siguiente manera:
Usando el modelo gravitacional de Newton, los planetas se atraen entre sí con una fuerza proporcional a sus masas e inversamente proporcional al cuadrado de sus distancias. Por otro lado, las leyes de Newton dicen que la aceleración de un cuerpo es proporcional a la suma de fuerzas que actúan sobre el cuerpo. Por lo tanto, en teoría por medio de estas leyes podríamos describir exactamente el movimiento de los cuerpos del sistema.
Estas leyes se traducen matemáticamente en lo que se denomina un sistema de ecuaciones diferenciales, por lo que para obtener el resultado solo deberíamos resolver estas ecuaciones. El gran problema es que, si bien está matemáticamente probado que todo sistema de este tipo tiene una solución, encontrar la solución es generalmente “imposible”.
El problema consistía en resolver dichas ecuaciones y así resolver la pregunta de si el movimiento del Sistema Solar es estable o inestable.
Volviendo al problema original, para hacerse una idea, si tenemos 2 cuerpos, por ejemplo la Tierra y la Luna, el movimiento estable descrito por este sistema es relativamente simple: si ambos sistemas tienen una velocidad inicial suficiente, el menor cuerpo (la Luna) gira alrededor del mayor (la Tierra).
Si pasamos 3 cuerpos ya las ecuaciones se vuelven mucho más complicadas de resolver.
Poincaré presentó una solución, demostrando entre varias cosas que dicho sistema no podía ser resuelto cuantitativamente, e inició la teoría moderna de ecuaciones diferenciales, la teoría cualitativa. En dicho trabajo probó cierta estabilidad del sistema en el caso de 3 cuerpos y ganó el concurso.
Pero otro matemático, editor de la revista en la cual sería publicado dicho trabajo, no se convenció de la prueba. Le comunicó esto a Poincaré, quien, tratando de explicarlo, encontró un error en su propio trabajo que no lo anulaba todo pero sí una parte sustancial sobre la estabilidad del sistema.
Trabajando para corregir este error Poincaré descubre lo que actualmente se denomina como “intersección homoclínica transversal de variedades estables e inestables”, fenómeno que da origen al “caos”.
¿Qué es un sistema caótico?
Para describir brevemente qué es un sistema caótico primero vamos a describir un sistema no caótico mediante un ejemplo:
Supongamos que tenemos un círculo y cada punto del círculo gira a velocidad constante. Por lo tanto, si queremos describir el movimiento de un punto, basta tomar el punto y luego de un tiempo t el punto se movió un ángulo igual al producto de la velocidad por este tiempo. En particular, si al escoger nuestro punto inicial “erramos” y escogemos un punto cercano, la diferencia del recorrido de este nuevo punto no será grande respecto al original, pues como ambos puntos se mueven igual, este error al escoger se mantendrá igual con el tiempo.
Un sistema caótico es un sistema donde, por más pequeño que sea nuestro error inicial al elegir el punto de partida, en un momento ambos puntos se encontrarán a una distancia considerablemente mayor que este error inicial.
Estas propiedades son muy importantes cuando uno quiere estudiar por ejemplo un modelo físico. Como generalmente no se puede medir con exactitud las posiciones iniciales de dicho sistema, la caoticidad del mismo puede hacer que nuestra predicción pierda validez muy rápidamente. Esto se denomina efecto mariposa por uno de los ejemplos clásicos de un sistema caótico: el clima.
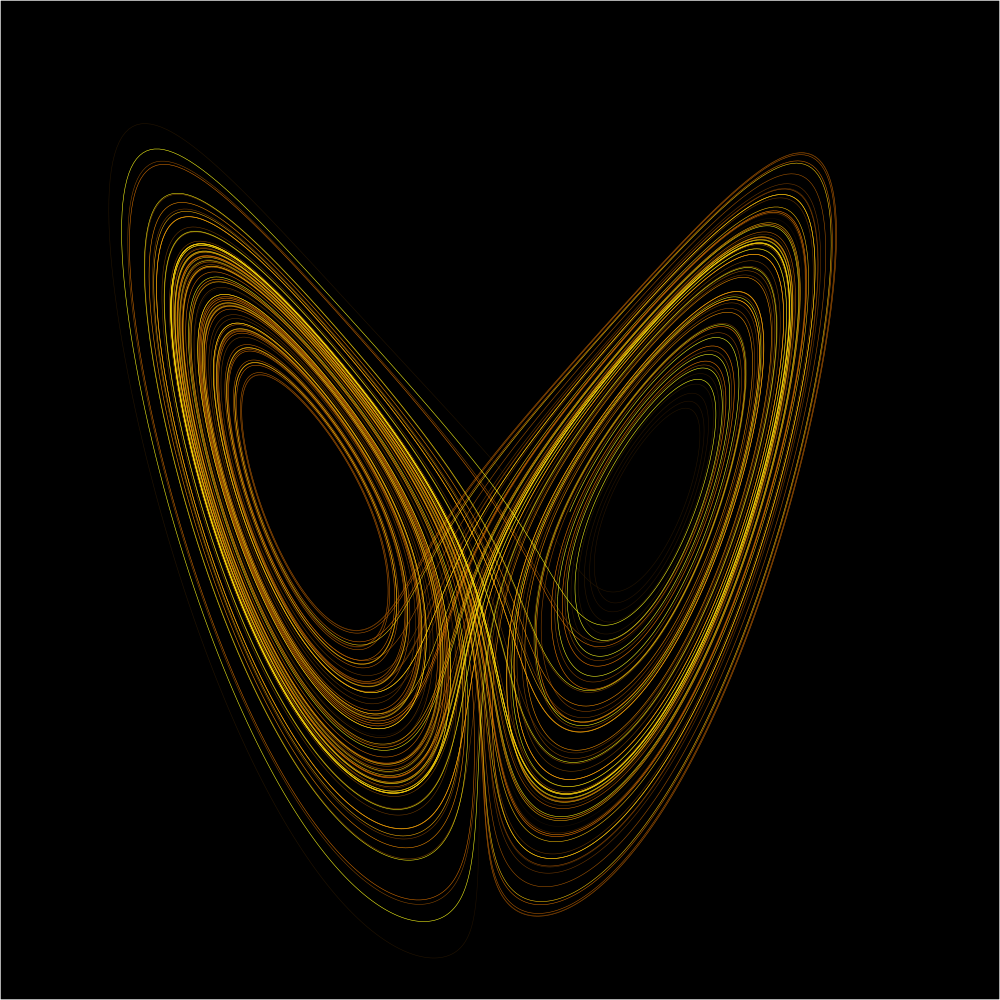
Que el clima es un sistema caótico fue observado por Lorenz en un famoso trabajo estudiando ecuaciones simplificadas del modelo climático, de allí el origen de la frase “el aleteo de una mariposa en Asunción (o Buenos Aires o Santiago) puede ocasionar un huracán en China”. Esto quiere decir que una pequeña diferencia en la condición inicial del sistema (el aleteo de la mariposa) puede ocasionar una diferencia grande en el futuro (el huracán).
Es justamente éste el fenómeno que aparecen en el modelo que descubrió Poincaré. Este trabajo y en particular el error de Poincaré dieron origen a un área de investigación en matemáticas llamada sistemas dinámicos.
En los últimos tiempos grandes trabajos se realizaron en esta área, entre los cuales se destacan los de la escuela brasileña en el Instituto de Matemática Pura e Aplicada (IMPA) en Río de Janeiro. En 2014 uno de sus investigadores, el brasileño Artur Ávila, fue el primer sudamericano y primer matemático formado en un instituto en un país considerado del tercer mundo en ganar la medalla Fields, máximo premio de las matemáticas.
En los últimos años se formó un nexo entre este instituto y Paraguay. Hasta ahora 3 doctores en matemática, entre ellos quien escribe, fuimos formados allí, y varios nuevos alumnos paraguayos se encuentran realizando sus estudios de maestría y doctorado en dicho instituto.
¿Qué te pareció este artículo?
Columnista de matemática de Ciencia del Sur. Es egresado de la Facultad de Ingeniería de la Universidad Nacional de Asunción. Realizó sus estudios de maestría en matemática aplicada y doctorado en matemáticas en el Instituto Nacional de Matemática Pura y Aplicada (IMPA) de Río de Janeiro, Brasil.
Sus primeros estudios posdoctorales también los ejecutó en el IMPA. Actualmente, realiza investigación posdoctoral en la Université de Paris 13, Francia.








 (35 votos, promedio: 4,74 de 5)
(35 votos, promedio: 4,74 de 5)







El articulo esta muy interesante pero justo cuando parece que va a explicar datos acerca del IMPA, termina de repente
Yo también esperaba contenido, no un trozo de currículum
Cual seria otro ejemplo de un sistema caótico?
el pendulo doble
Ricardo – Un ejemplo sencillo de sistema caótico es si tomas una calculadora y escribes 1,1 y aprietas continuamente la tecla «elevar al cuadrado». Al poco tiempo el valor irá subir tanto que la maquina dará «error» por mayor que sea su capacidad de calculo.
Entonces dices «que pasa si tomo algo mas próximo del 1, por ejemplo 1,01»? te darás cuenta que igualmente al apretar continuamente la tecla «elevar al cuadrado» la maquina va a tardar más, pero igual va a dar error.
Entonces dices «que pasa si tomo algo mas próximo del 1, por ejemplo 1,0001»? te darás cuenta que igualmente al apretar continuamente la tecla «elevar al cuadrado» la maquina va a tardar mas, pero igual va a dar error.
Y así, por mas que te aproximes de 1 (o sea por menor que sea el desvío de 1), siempre la maquina dará «error», lo único es que tardará mas tiempo en acontecer.
Ese es un sistema caótico.
Dr. Poletti: os felicito por la transparencia del artículo. Debemos insistir en la divulgación masiva de nuestra amada matemática. Fomentar en nuestra niñez la curiosidad y el manejo lúdico de los números, y en un futuro no muy lejano las legiones de matemáticos se incrementará.