Deseaba ver el infinito, pero en realidad nunca salía de los límites de su propia cabeza.
La luz fantástica, Terry Pratchett (1986)
Usualmente se relaciona al infinito con un tamaño sin límites, siendo una pregunta clásica si nuestro Universo posee límites en el tiempo y espacio, o al contrario es infinito. Otra forma de imaginar al infinito es a través de objetos de tamaño finito y preguntándonos si tales objetos finitos están compuestos por infinitos objetos infinitamente pequeños, hasta el momento hay un límite en la escala de partículas subatómicas que podemos estudiar.
Por último, también se piensa en el infinito a través de la acción, donde nos preguntamos si una acción tiene un número limitado o ilimitado de formas, por ejemplo, si existen infinitas secuencias de letras posibles y potencialmente infinitos libros que podrían escribirse.
A pesar de lo abrumador y hasta metafísico que sea el infinito, se puede decir que hubo un progreso en su comprensión y no estamos parados en el mismo punto que los antiguos griegos, al menos en nuestra comprensión matemática del infinito. A continuación, daremos un breve vistazo a lo que la matemática moderna puede decirnos del infinito y si estas conclusiones tienen alguna consecuencia en el mundo real.
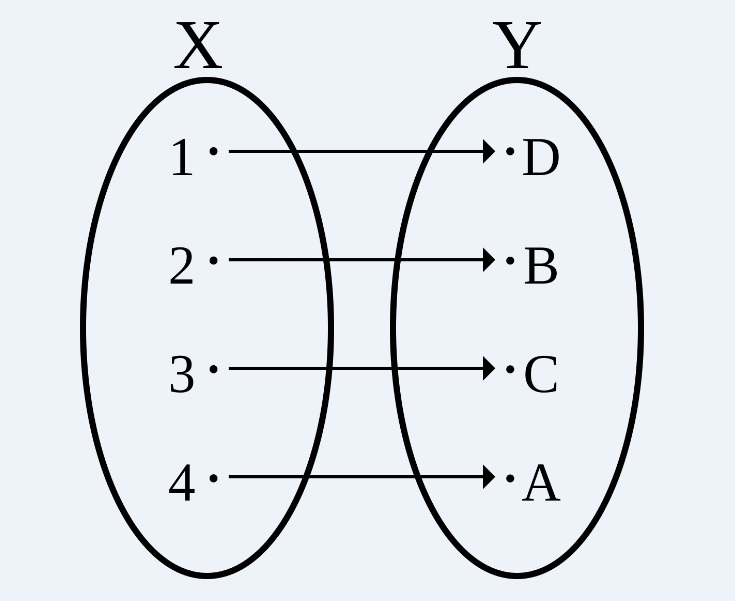
Si deseamos constatar que dos conjuntos finitos poseen el mismo número de elementos, es suficiente con ver si a cada elemento del primer conjunto le puedo asignar un único elemento irrepetible del segundo conjunto, de modo que a cada elemento del segundo conjunto también le toca un único elemento irrepetible del primer conjunto.
Si existe esa asignación de elementos entre dos conjuntos, decimos que existe una biyección entre tales conjuntos. Por ejemplo, existe una biyección entre 7 niños y 7 manzanas porque a cada niño le toca una manzana y a cada manzana un niño. No así entre 8 niños y 7 manzanas siendo que un niño se quedaría sin manzana.
¿Qué pasaría si usamos biyecciones para comparar conjuntos infinitos? Por ejemplo, el conjunto de los números naturales A: 1,2,3,4,5,6,…, el conjunto de los números naturales pares B:2,4,6,8,… y el conjunto de los números naturales impares C: 1,3,5,7,9,11,… Para cada número natural i existe un número natural par 2*i y para cada natural par 2*i un número natural i.
También para cada número natural i existe un número impar 2*i-1 y para cada número impar 2*i-1 existe un número natural i. ¿Entonces los conjuntos A, B, C tienen el mismo tamaño? Nótese que B y C son subconjuntos o «pedazos» de A. ¿Entonces A tiene el mismo tamaño que un pedazo de sí mismo? Además, observamos que juntando B y C obtenemos A. ¿Entonces A es igual a dos veces él mismo? ¿1+1=1?
De hecho, sea cualquier número primo p, para cada número natural i podemos asignarle una potencia de p (es decir p^i). Nótese que si dos primos p y q son distintos los conjuntos de potencias para cada primo no comparten ningún solo elemento. Entonces como existen infinitos números primos y cada conjunto de potencias tiene una biyección con los naturales. ¿Podemos meter infinitos conjuntos del tamaño de los números naturales dentro de los mismos números naturales?
Estas paradojas fueron explicadas por David Hilbert con su analogía del «Hotel infinito» [1], aunque fue George Cantor el matemático que más exploró estas propiedades de los conjuntos infinitos [2].
Hasta ahora puede parecer que podemos definir una biyección entre cualquier par de conjuntos infinitos, por ejemplo, se sabe que existen biyecciones entre los puntos de una recta y un cuadrado [3]. Pero el mismo George Cantor demostró que no existe una biyección entre los números naturales y los números reales.
Por lo tanto, podemos decir que el conjunto de los reales es un conjunto infinito «más grande» que el infinito conjunto de los números naturales [4]. De hecho, sea un conjunto cualquiera X, llamamos conjunto de partes al conjunto de todos los subconjuntos de X. Por ejemplo, si X={0,1,2}, entonces el conjunto de partes de X seria P(X)={{},{0},{1},{2},{1,2},{1,
Si un conjunto finito tiene tamaño n entonces su conjunto de partes tiene tamaño 2^n, evidentemente no existe biyección entre un conjunto finito y su conjunto de partes ¿pero es lo mismo para los conjuntos infinito? Sí, Cantor también demostró que no existe biyección entre un conjunto infinito y su conjunto de partes [5]. Con eso podemos deducir que no existe un conjunto infinito que sea mayor a todos los demás infinitos.
Pues si A es el mayor puedo dar por seguro que su conjunto de partes P(A) es mayor aún, además que es mayor a P(A) su mismo conjunto de partes P(P(A)) y así sucesivamente.
¿Esto va más allá de una curiosidad matemática?
¿De qué puede servir?
Los amantes de las ciencias puras encontrarán interesante todo lo expuesto, pero los más aplicados dirán ¿para qué esto puede servir? Veamos un ejemplo para computación. Un problema de decisión es aquella pregunta donde la solución es un sí o un no, por ejemplo ¿El valor de determinado cálculo supera 10? ¿Determinada secuencia de números contiene un 0? ¿El valor de esta función supera 100 en algún punto?, etcétera.
Prácticamente todos esos problemas pueden ser codificados con ceros y unos para que un programa los procese y les dé una respuesta que puede ser 1 para un sí y 0 para un no. Más aún, el mismo programa puede ser codificado con ceros y unos. En ese sentido un problema en computación puede representarse como cada una de las salidas correctas que corresponden a cada posible entrada (recordamos que entrada son los datos que meto en el programa y salida es la correspondiente respuesta del programa).
Por lo que podemos representar cada problema de decisión como una secuencia de ceros y unos infinita porque la cantidad de posibles entradas es infinita, además el conjunto de secuencias infinitas de ceros y unos posee una biyección con los números reales.
En cambio, los programas de computación tienen un tamaño finito y podemos representar el conjunto de todos los posibles programas como el conjunto de secuencias de ceros y unos de tamaño finito, este conjunto posee una biyección con los números naturales.
Ahora bien, para que exista un programa correcto para cada posible problema de decisión, debe existir una biyección entre una parte del conjunto de todos los programas y el conjunto de todos los problemas de decisión. Lo cual es imposible porque el conjunto de programas tiene el tamaño de los números naturales, pero el conjunto de problemas tiene el tamaño de los números reales y sabemos que ambos son infinitos de distinto tamaño. [7]
La teoría de Cantor actualmente es aceptada por la comunidad matemática como un conocimiento básico para la ciencia, sin embargo, en su época fue duramente criticada por matemáticos constructivistas finitistas que solo aceptaban verdades matemáticas a partir de objetos que pueden ser «construidos» y argumentaban que el infinito no cumple con ese requisito [6].
Se especula que el mismo Cantor terminó en un psiquiátrico agobiado tanto por las paradojas como las críticas a su trabajo. Más allá de las matemáticas, la teoría de Cantor puede dar argumentos interesantes al análisis filosófico y a las ciencias empíricas.
Volviendo a nuestra introducción, no es necesario que el universo sea infinito para aplicar las ideas de Cantor, podemos ver el infinito como el potencial de formas en que objetos finitos pueden configurarse, como hicimos al considerar todos los programas de computación.
De esa forma el infinito emerge como un ente que no pierde sentido en un universo potencialmente finito.

Referencias
[2] BBVA Open Mind (2019). Georg Cantor, el hombre que descubrió distintos infinitos.
[3] Bijection between unit interval and unit square.
[4] The Set of Real Numbers is Uncountable.
[5] Conjunto Potencia.
[6] Solaeche Galera, MC. (1995). La Controversia entre L. Kronecker y G. Cantor acerca del Infinito. Universidad del Zulia.
[7] Lewis, H. and Papadimitriou, C. (1998). Elements of theory of computation.
¿Qué te pareció este artículo?
Sebastián Alberto Grillo es licenciado en matemática pura y máster en ciencias de la computación por la Universidad Nacional de Asunción (UNA). Es doctor en ciencias de la computación por la Universidad Federal de Río de Janeiro, Brasil. Investigador en matemática aplicada, computación teórica e inteligencia artificial. Está categorizado en el PRONII nivel I del CONACYT. En Ciencia del Sur es columnista de matemática, ciencias de la computación y educación.








 (8 votos, promedio: 4,75 de 5)
(8 votos, promedio: 4,75 de 5)